题目内容
若等腰梯形的下底与对角线长相等，上底与高相等，则上底与下底之比是（ ）
分析：首先根据题意作出图形，然后由等腰梯形的性质与勾股定理，可求得答案．
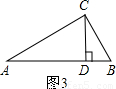
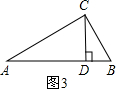
解答：
解：如图，梯形ABCD中，AD∥BC，AB=CD，AE⊥BC于点E，DF⊥BC于点F，BD=BC，AD=AE=DF，
∴四边形ADFE是正方形，AE=DF，
∵在Rt△ABE和Rt△DCF中，
，
∴Rt△ABE≌Rt△DCF（HL），
∴BE=CF，
设AD=a，BE=b，
则DF=AD=a，CF=BE=b，BC=BE+EF+CF=a+2b，
∴BD=a+2b，BF=BE+EF=a+b，
在Rt△BDF中，BD2=BF2+DF2，
即（a+2b）2=（a+b）2+a2，
即a2-2ab-3b2=0，
∴（a+b）（a-3b）=0，
解得：a=3b，
∴AD：BC=a：（a+2b）=3b：5b=3：5．
故选D．
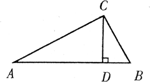
解：如图，梯形ABCD中，AD∥BC，AB=CD，AE⊥BC于点E，DF⊥BC于点F，BD=BC，AD=AE=DF，∴四边形ADFE是正方形，AE=DF，
∵在Rt△ABE和Rt△DCF中，
|
∴Rt△ABE≌Rt△DCF（HL），
∴BE=CF，
设AD=a，BE=b，
则DF=AD=a，CF=BE=b，BC=BE+EF+CF=a+2b，
∴BD=a+2b，BF=BE+EF=a+b，
在Rt△BDF中，BD2=BF2+DF2，
即（a+2b）2=（a+b）2+a2，
即a2-2ab-3b2=0，
∴（a+b）（a-3b）=0，
解得：a=3b，
∴AD：BC=a：（a+2b）=3b：5b=3：5．
故选D．
点评：此题考查了等腰梯形的性质、勾股定理以及全等三角形的判定与性质．此题难度适中，注意掌握数形结合思想与方程思想的应用．
练习册系列答案
相关题目
这种分割称为黄金分割，点C叫做线段AB的黄金分割点．
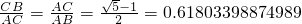．这种分割称为黄金分割，点C叫做线段AB的黄金分割点．类似地我们可以定义，顶角为36°的等腰三角形叫黄金三角形，其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点．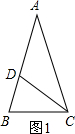
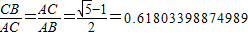．这种分割称为黄金分割，点C叫做线段AB的黄金分割点．类似地我们可以定义，顶角为36°的等腰三角形叫黄金三角形，其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点．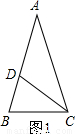
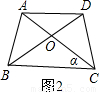
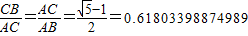．这种分割称为黄金分割，点C叫做线段AB的黄金分割点．类似地我们可以定义，顶角为36°的等腰三角形叫黄金三角形，其底与腰之比为黄金数，底角平分线与腰的交点为腰的黄金分割点．
