题目内容
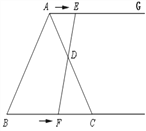
【题目】如图,![]() 中,
中,![]() 垂足是D,AE平分
垂足是D,AE平分![]() ,交BC于点E,在
,交BC于点E,在![]() 外有一点F,使
外有一点F,使![]() .
.
(1)求∠ACF的度数;
(2)求证:![]() ;
;
(3)在AB上取一点M,使![]() ,连接MC,交AD于点N,连接ME.求证:
,连接MC,交AD于点N,连接ME.求证:![]() .
.
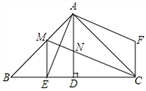
【答案】(1)45°;(2)证明见解析;(3)证明见解析.
【解析】试题分析:(1)根据等腰直角三角形的性质求出∠B=∠ACB=45°,再求出∠ACF=45°;
(2)由∠B =45°,∠ACF=45°,得到∠B=∠ACF,根据同角的余角相等求出∠BAE=∠CAF,然后利用“角边角”证明△ABE和△ACF全等,根据全等三角形对应边相等证明即可;
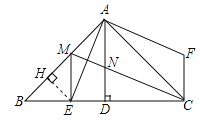
(3)过点E作EH⊥AB于H,求出△BEH是等腰直角三角形,然后求出HE=BH,再根据角平分线上的点到角的两边距离相等可得DE=HE,然后求出HE=HM,从而得到△HEM是等腰直角三角形,再根据等腰直角三角形的性质求解即可.
试题解析:(1)∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,∵FC⊥BC,∴∠BCF=90°,∴∠ACF=90°﹣45°=45°;
(2)∵∠B =45°,∠ACF=45°,∴∠B=∠ACF.
∵∠BAC=90°,FA⊥AE,∴∠BAE+∠CAE=90°,∠CAF+∠CAE=90°,∴∠BAE=∠CAF.
在△ABE和△ACF中,∵∠BAE=∠CAF,AB=AC,∠B=∠ACF
∴△ABE≌△ACF(ASA),∴BE=CF;
(3)如图,过点E作EH⊥AB于H,则△BEH是等腰直角三角形,∴HE=BH,∠BEH=45°.
∵AE平分∠BAD,AD⊥BC,∴DE=HE,∴DE=BH=HE.
∵BM=2DE,∴HE=HM,∴△HEM是等腰直角三角形,∴∠MEH=45°,∴∠BEM=45°+45°=90°,∴ME⊥BC.

【题目】小敏参加了某次演讲比赛,根据比赛时七位评委所给的分数制作了如下表格:
平均数/分 | 中位数/分 | 众数/分 | 方差/分2 |
8.8 | 8.9 | 8.5 | 0.14 |
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数B.中位数C.众数D.方差