题目内容
将矩形纸片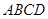 对折, 使点B与点D重合,折痕为
对折, 使点B与点D重合,折痕为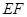 ,连结
,连结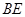 ,则与线段
,则与线段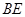 相等的线段条数(不包括BE,不添加辅助线)有 ( )
相等的线段条数(不包括BE,不添加辅助线)有 ( )
 对折, 使点B与点D重合,折痕为
对折, 使点B与点D重合,折痕为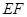 ,连结
,连结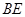 ,则与线段
,则与线段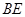 相等的线段条数(不包括BE,不添加辅助线)有 ( )
相等的线段条数(不包括BE,不添加辅助线)有 ( )| A.1 | B.2 | C.3 | D.4 |

B
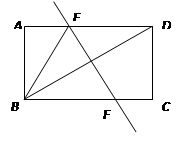
首先由将矩形纸片ABCD对折,使点B与点D重合,折痕为EF,即可得EF是BD的垂直平分线,则可得DE=BE,又由矩形的性质,可证得:△ODE≌△OBF,则可得DE=BF,则可知与BE相等的线段有DE与BF.
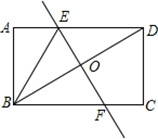
解:将矩形纸片ABCD对折,使点B与点D重合,折痕为EF,
∴BE=DE,OB=OD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EDB=∠DBF,∠OED=∠OFB,
∴△ODE≌△OBF(AAS),
∴DE=BF,
∴BE=DE=BF.
∴与线段BE相等的线段条数(不包括BE,不添加辅助线)有2条.
故选B.
此题考查了折叠的性质,矩形的性质,全等三角形的判定与性质,以及垂直平分线的性质等知识.此题综合性较强,但难度不大,解题时要注意数形结合思想的应用.

解:将矩形纸片ABCD对折,使点B与点D重合,折痕为EF,
∴BE=DE,OB=OD,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EDB=∠DBF,∠OED=∠OFB,
∴△ODE≌△OBF(AAS),
∴DE=BF,
∴BE=DE=BF.
∴与线段BE相等的线段条数(不包括BE,不添加辅助线)有2条.
故选B.
此题考查了折叠的性质,矩形的性质,全等三角形的判定与性质,以及垂直平分线的性质等知识.此题综合性较强,但难度不大,解题时要注意数形结合思想的应用.

练习册系列答案
相关题目
 形的边长为1.位于AD中点处的光点P按图18-2的程序移动
形的边长为1.位于AD中点处的光点P按图18-2的程序移动
 的路径总长(结果保留π)
的路径总长(结果保留π)
 ,求S与
,求S与
 2.
2. 


