题目内容
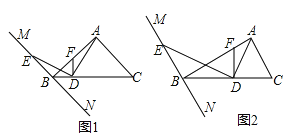
【题目】等腰Rt△ABC中,∠BAC=90°,点A、点B分别是y轴、x轴上的两个动点,点C在第三象限,直角边AC交x轴于点D,斜边BC交y轴于点E.
(1)若A(0,1),B(2,0),画出图形并求C点的坐标;
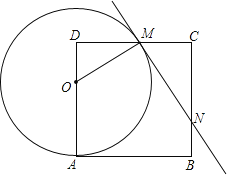
(2)若点D恰为AC中点时,连接DE,画出图形,判断∠ADB和∠CDE大小关系,说明理由.
【答案】(1)作图见解析,C(﹣1,﹣1);(2)∠ADB=∠CDE.理由见解析.
【解析】
(1)过点C作CF⊥y轴于点F通过证明△ACF≌△BAO得CF=OA=1,AF=OB=2,求得OF的值,就可以求出C的坐标;
(2)过点C作CG⊥AC交y轴于点G,先证明△ACG≌△BAD就可以得出CG=AD=CD,∠DCE=∠GCE=45°,再证明△DCE≌△GCE就可以得出结论.
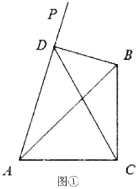
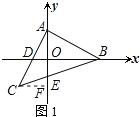
解:(1)过点C作CF⊥y轴于点F,如图1所示:
 ,
,
∴∠AFC=90°,
∴∠CAF+∠ACF=90°.
∵△ABC是等腰直角三角形,∠BAC=90°,
∴AC=AB,∠CAF+∠BAO=90°,∠AFC=∠BAC,
∴∠ACF=∠BAO.
在△ACF和△BAO中,
∵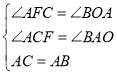 ,
,
∴△ACF≌△BAO(AAS),
∴CF=OA=1,AF=OB=2,
∴OF=1,
∴C(﹣1,﹣1);
(2)∠ADB=∠CDE.理由如下:
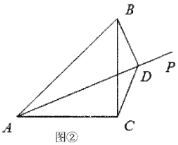
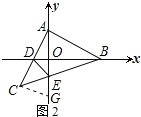
证明:过点C作CG⊥AC交y轴于点G,如图2所示:
 ,
,
∴∠ACG=∠BAC=90°,
∴∠AGC+∠GAC=90°.
∵∠CAG+∠BAO=90°,
∴∠AGC=∠BAO.
∵∠ADO+∠DAO=90°,∠DAO+∠BAO=90°,
∴∠ADO=∠BAO,
∴∠AGC=∠ADO.
在△ACG和△BAD中,
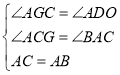 ,
,
∴△ACG≌△BAD(AAS),
∴CG=AD=CD.
∵∠ACB=∠ABC=45°,
∴∠DCE=∠GCE=45°,
在△DCE和△GCE中,
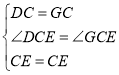 ,
,
∴△DCE≌△GCE(SAS),
∴∠CDE=∠CGE,
∴∠ADB=∠CDE.

 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案