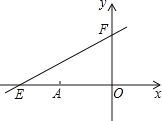
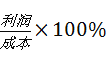��Ŀ����
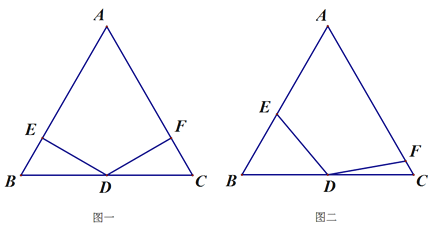
����Ŀ���ڵȱߡ�ABC�У���D���߶�BC���е㣬��EDF=120�㣬�߶�DE���߶�AB�ཻ�ڵ�E.�߶�DF���߶�AC�ཻ�ڵ�F.
��1����ͼһ����DF��AC����ֱ��д��DE��AB��λ�ù�ϵ��
��2�����ж�DE��DF��������ϵ.��д����������.
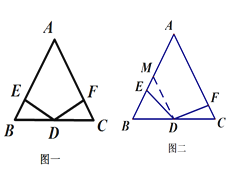
��3����ͼ��������1���еġ�EDF�Ƶ�D˳ʱ����תһ���ĽǶȣ�DF�����߶�AC�ཻ�ڵ�F. ��2���еĽ��ۻ���������������д��֤�����̣�����������˵������.
��4���ڡ�EDF�Ƶ�D˳ʱ����ת�����У�ֱ���õ�ʽ��ʾ�߶�BE��CF��AB֮���������ϵ��
���𰸡���1��DE��AB����2��DE=DF ֤������������3������.֤������������4��BE+CF=![]()
�������������������1��DE��AB�������ı��ε��ڽǺͶ���������á�AED=90�㣬����DE��AB����2�������ٿ���ͨ��AAS֤����BED�ա�CFD���ó����ۣ����� ��Ҳ��������ADͨ���������������ߺ�һ�ó�ADƽ�֡�BAC�����ý�ƽ�������ʶ����ó�����3��������֤���������ٿ��Իָ���ͼһ����ͼһ�Ļ�����֤��ȫ�ȵó����ۣ�������Ҳ����ȡAB�е�M������DM֤����EDM�ա�FDC��������4��ȡAB�е�M������DM֤����EDM�ա�FDC���ɵý���.
���������
��1��DE��AB
��2��DE=DF ֤�����ٿ���ͨ��AAS֤����BED�ա�CFD���ó�����
��Ҳ��������ADͨ���������������ߺ�һ�ó�ADƽ�֡�BAC�����ý�ƽ�������ʶ����ó�.
����.֤���ٿ��Իָ���ͼһ����ͼһ�Ļ�����֤��ȫ�ȵó�����.
��Ҳ����ȡAB�е�M������DM֤����EDM�ա�FDC����.
��4��BE+CF=![]()

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�