题目内容
若双曲线y=
(k≠0)的两个分支在第二、四象限内，则抛物线y=kx2-2x+k2的图象大致是图中的（ ）
| k |
| x |
A、 |
B、 |
C、 |
D、 |
分析：根据双曲线y=
(k≠0)的图象位置可知k＜0；再根据k的符号判断抛物线的开口方向及对称轴．
| k |
| x |
解答：解：∵双曲线y=
(k≠0)的两个分支在第二、四象限内，即k＜0，
∴抛物线开口向下，
对称轴x=-
=
＜0，对称轴在y轴的左边．故选A．
| k |
| x |
∴抛物线开口向下，
对称轴x=-
| -2 |
| 2k |
| 1 |
| k |
点评：本题考查了反比例函数图象的性质和二次函数系数与抛物线形状的关系．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
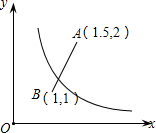已知点A（1.5，2）、B（1，1），若双曲线y=| k |
| x |
| A、1≤k≤3 |
| B、1≤k≤2 |
| C、1≤k≤1.5 |
| D、k≥3或k≤1 |
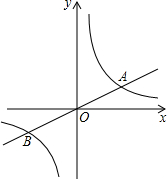如图，直线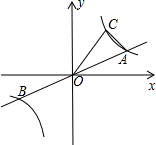
如图，已知直线y=