题目内容
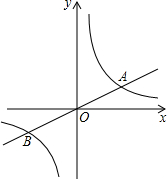 如图,直线y=
如图,直线y=| 1 |
| 2 |
| k |
| x |
(1)求k的值;
(2)若双曲线y=
| k |
| x |
分析:(1)先将点A的横坐标4代入直线y=
x,求得点A的坐标,再代入双曲线y=
,求出k的值;
(2)先求得点C的坐标,从而得到△AOD的底边长OD=8,OD上的高为2,求得S△AOD.
| 1 |
| 2 |
| k |
| x |
(2)先求得点C的坐标,从而得到△AOD的底边长OD=8,OD上的高为2,求得S△AOD.
解答:解:(1)x=4代入y=
x可得:A(4,2),
将(4,2)代入y=
可得:k=8.
(2)y=1代入y=
可得:C(8,1),
△AOD中,OD=8,OD上的高为2.
∴S△AOD=
×8×2=8.
| 1 |
| 2 |
将(4,2)代入y=
| k |
| x |
(2)y=1代入y=
| 8 |
| x |
△AOD中,OD=8,OD上的高为2.
∴S△AOD=
| 1 |
| 2 |
点评:主要考查了待定系数法求反比例函数的解析式和反比例函数y=
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
| k |
| x |

练习册系列答案
相关题目
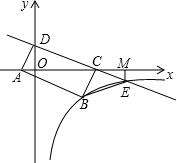 如图,直线y=-
如图,直线y=-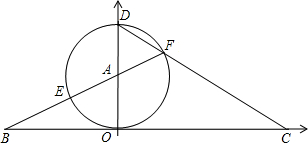 D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B.
D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B.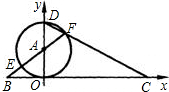 如图,直线y=-
如图,直线y=-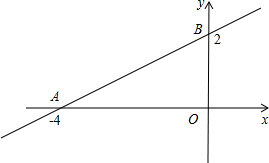 如图,直线y=
如图,直线y= (2013•蒙山县一模)如图,直线
(2013•蒙山县一模)如图,直线