题目内容
若实数a、b、c、d满足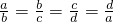 ,则
,则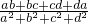 的值是
的值是
- A.1或0
- B.-1或0
- C.1或-2
- D.1或-1
D
分析:先设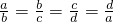 =k,从而得出k=±1,再分两种情况讨论即可.
=k,从而得出k=±1,再分两种情况讨论即可.
解答:设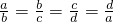 =k,
=k,
则b2=ac,c2=bd,d2=ac=b2,a2=bd=c2,
由 =k得,a=bk,
=k得,a=bk,
由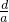 =k得,d=ak=bk2,
=k得,d=ak=bk2,
由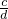 =k得,c=dk=bk3,
=k得,c=dk=bk3,
再由 =k得,
=k得,
 =k,
=k,
即:k4=1,
k=±1.
当k=1时,原式=1;
当k=-1时,原式=-1;
故选D.
点评:本题考查了分式的化简求值,解题的关键是设已知分式为定值,再求解就容易了.
分析:先设
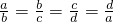 =k,从而得出k=±1,再分两种情况讨论即可.
=k,从而得出k=±1,再分两种情况讨论即可.解答:设
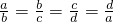 =k,
=k,则b2=ac,c2=bd,d2=ac=b2,a2=bd=c2,
由
 =k得,a=bk,
=k得,a=bk,由
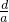 =k得,d=ak=bk2,
=k得,d=ak=bk2,由
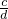 =k得,c=dk=bk3,
=k得,c=dk=bk3,再由
 =k得,
=k得, =k,
=k,即:k4=1,
k=±1.
当k=1时,原式=1;
当k=-1时,原式=-1;
故选D.
点评:本题考查了分式的化简求值,解题的关键是设已知分式为定值,再求解就容易了.

练习册系列答案
相关题目