题目内容
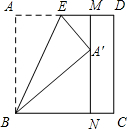 如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M、N分别是AD、BC边上距DC最近的n等分点(n≧2,且n为整数),则A′N=
如图,正方形纸片ABCD的边长为1,M、N分别是AD、BC边上的点,将纸片的一角沿过点B的直线折叠,使A落在MN上,落点记为A′,折痕交AD于点E,若M、N分别是AD、BC边上距DC最近的n等分点(n≧2,且n为整数),则A′N=
| ||
| n |
| ||
| n |
分析:首先由若M、N分别是AD、BC边上距DC最近的n等分点(n≥2,且n为整数),可得BN=
,CN=
,然后利用勾股定理即可求得答案.
| n-1 |
| n |
| 1 |
| n |
解答:解:∵四边形ABCD是正方形,
∴AB=BC=1,∠A=90°,
由折叠的性质得:A′B=AB=1,∠A′NB=∠A=90°,
由题意得:若M,N分别是AD,BC边的上距DC最近的n等分点(n≥2,且n为整数),
即把BC分成n等份,BN占n-1份,
∴BN=
,CN=
,
在Rt△A′BN中,根据勾股定理,A′N=
=
(n≥2,且n为整数).
故答案为:
.
∴AB=BC=1,∠A=90°,
由折叠的性质得:A′B=AB=1,∠A′NB=∠A=90°,
由题意得:若M,N分别是AD,BC边的上距DC最近的n等分点(n≥2,且n为整数),
即把BC分成n等份,BN占n-1份,
∴BN=
| n-1 |
| n |
| 1 |
| n |
在Rt△A′BN中,根据勾股定理,A′N=
12-(
|
| ||
| n |
故答案为:
| ||
| n |
点评:此题考查了折叠的性质、正方形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用,注意掌握折叠前后图形的对应关系.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 (2013•昆山市二模)如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为
(2013•昆山市二模)如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为 (2012•宽城区一模)如图,正方形纸片ABCD,对角线AC、BD交于点O,折叠纸片,使AD落在BD上,点A恰好与BD上的点F重合,展开纸片后,折痕DE分别交AB、AC于点E、G,则∠AGD的度数为
(2012•宽城区一模)如图,正方形纸片ABCD,对角线AC、BD交于点O,折叠纸片,使AD落在BD上,点A恰好与BD上的点F重合,展开纸片后,折痕DE分别交AB、AC于点E、G,则∠AGD的度数为 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.