题目内容
 (2012•宽城区一模)如图,正方形纸片ABCD,对角线AC、BD交于点O,折叠纸片,使AD落在BD上,点A恰好与BD上的点F重合,展开纸片后,折痕DE分别交AB、AC于点E、G,则∠AGD的度数为
(2012•宽城区一模)如图,正方形纸片ABCD,对角线AC、BD交于点O,折叠纸片,使AD落在BD上,点A恰好与BD上的点F重合,展开纸片后,折痕DE分别交AB、AC于点E、G,则∠AGD的度数为112.5°
112.5°
.分析:由四边形ABCD是正方形,可得∠OAD=∠ODA=45°,又由折叠的性质可得:∠ADE=∠EDF=
∠ADO=22.5°,然后由三角形的内角和定理求得答案.
| 1 |
| 2 |
解答:解:∵四边形ABCD是正方形,
∴∠OAD=∠ODA=45°,
由折叠的性质可得:∠ADE=∠EDF=
∠ADO=22.5°,
∴∠AGD=180°-∠OAD-∠ADE=180°-45°-22.5°=112.5°.
故答案为:112.°.
∴∠OAD=∠ODA=45°,
由折叠的性质可得:∠ADE=∠EDF=
| 1 |
| 2 |
∴∠AGD=180°-∠OAD-∠ADE=180°-45°-22.5°=112.5°.
故答案为:112.°.
点评:此题考查了正方形的性质、折叠的性质以及三角形内角和定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 (2012•宽城区一模)某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图①所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.如图②,当∠BAC=18°时,CD⊥AB于D,求支撑臂CD的长.
(2012•宽城区一模)某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图①所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.如图②,当∠BAC=18°时,CD⊥AB于D,求支撑臂CD的长.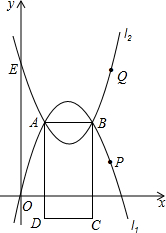 有两条抛物线l1、l2都经过A、B两点,且关于AB所在直线对称,其中抛物线l1经过原点,抛物线l2交y轴于点E.设P、Q两点分别在抛物线l1、l2上运动.
有两条抛物线l1、l2都经过A、B两点,且关于AB所在直线对称,其中抛物线l1经过原点,抛物线l2交y轴于点E.设P、Q两点分别在抛物线l1、l2上运动.