题目内容
25、(1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.
(2)依已知条件和(1)中的结论:
①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.

分析:(1)连接AC,BD,由同弧所对的圆周角相等与四边形的内角和为360°,即可证得∠A+∠BCD=180°;又由同角的补角相等,求得∠DCE=∠A;
(2)根据圆的内接四边形的对角互补与三角形的外角的性质,即可证得结论.
(2)根据圆的内接四边形的对角互补与三角形的外角的性质,即可证得结论.
解答:解:(1)

连接AC,BD,
则:∠1=∠4,∠2=∠7,∠3=∠6,∠5=∠8,
∴∠BAD+∠ABC+∠BCD+∠CDA=∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=2(∠1+∠2+∠5+∠6)=360°,
∴∠1+∠2+∠5+∠6=180°,
∴∠A+∠BCD=180°;
∵∠DCE+∠BCD=180°,
∴∠DCE=∠A;
(2)①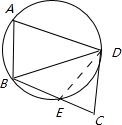
连接DE,
∵∠A+∠BED=180°,∠BDE>∠BCD,
∴∠A+∠BCD<180°;
②
延长DC交⊙O于点E,连接BE,
∵∠A+∠E=180°,∠BCD>∠E,
∴∠A+∠BCD>180°.

连接AC,BD,
则:∠1=∠4,∠2=∠7,∠3=∠6,∠5=∠8,
∴∠BAD+∠ABC+∠BCD+∠CDA=∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=2(∠1+∠2+∠5+∠6)=360°,
∴∠1+∠2+∠5+∠6=180°,
∴∠A+∠BCD=180°;
∵∠DCE+∠BCD=180°,
∴∠DCE=∠A;
(2)①

连接DE,
∵∠A+∠BED=180°,∠BDE>∠BCD,
∴∠A+∠BCD<180°;
②

延长DC交⊙O于点E,连接BE,
∵∠A+∠E=180°,∠BCD>∠E,
∴∠A+∠BCD>180°.
点评:此题考查了圆的内接四边形的对角互补的性质与证明,此题的图形变换比较多,所以要注意识图.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为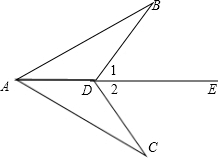 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为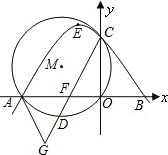 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧