题目内容
直角三角形ABC中，∠A=90°，AB=5cm，AC=4cm，则∠A的平分线AD的长为分析：做DE垂直AB于E，由∠A=90°，利用相似三角形的判定与性质求得AE，然后利用勾股定理即可求出AD的长．
解答：解：做DE垂直AB于E，由∠A=90°，得△BDE∽△BCA
由AD是∠A的平分线，则AE=DE，
=
=
=
=
，由AE=DE，得
=
即
=
，解得AE=
，
在直角三角形ADE中AD2=AE2+DE2，
所以AD=
．
故答案为：
由AD是∠A的平分线，则AE=DE，
| BE |
| AB |
| DE |
| AC |
| BE |
| DE |
| AB |
| AC |
| 5 |
| 4 |
| BE |
| AE |
| 5 |
| 4 |
| BE+AE |
| AE |
| 9 |
| 4 |
| 20 |
| 9 |
在直角三角形ADE中AD2=AE2+DE2，
所以AD=
20
| ||
| 9 |
故答案为：
20
| ||
| 9 |
点评：此题主要考查学生相似三角形的判定与性质和勾股定理的理解和掌握．还要应用到等式的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
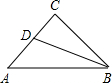如图，在等腰直角三角形ABC中，∠C=90°，AC=6，D是AC上一点，若tan∠DBA=
如图，在直角三角形ABC中，∠C=90°，AB=5，AC=3．点P、Q分别是BC边和AB边上的动点，点P从点C向点B运动，点Q从点A向点B运动，QR⊥BC，垂足为R，设P、Q同时运动，并且当P运动4x单位长度时，Q运动5（1-x）单位长度．是否存在x的值，使以P、Q、R为顶点的三角形与△ACP相似？若存在，求出所有x的值；若不存在，说明理由．
如图，等腰直角三角形ABC中，∠BAC=90°，D、E分别为AB、AC边上的点，AD=AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．
如图，直角三角形ABC中，∠ABC=90°，点D、E分别是AC、BC的中点，AB=3，BC=4，则DE和BD的长分别为（ ）