题目内容
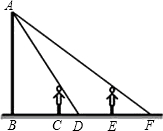
如图所示，小明为测量一棵树CD的高度，他在距树24m处立了一根高为2m的标杆EF，然后小明前后调整自己的位置，当他与树相距27m时，他的眼睛、标杆的顶端和树顶端在同一直线上．已知小明身高1.6m，求树的高度．
过点A作AN∥BD交CD于N，交EF于M，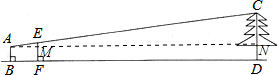
∵人、标杆、树都垂直于地面，
∴∠ABF=∠EFD=∠CDF=90°，
∴AB∥EF∥CD，
∴∠EMA=∠CNA，
∵∠EAM=∠CAN，
∴△AEM∽△ACN，
∴
=
，
∵AB=1.6m，EF=2m，BD=27m，FD=24m，
∴
=
，
解得：CN=3.6m，
则树的高度为3.6+1.6=5.2m．
∵人、标杆、树都垂直于地面，
∴∠ABF=∠EFD=∠CDF=90°，
∴AB∥EF∥CD，
∴∠EMA=∠CNA，
∵∠EAM=∠CAN，
∴△AEM∽△ACN，
∴
| EM |
| CN |
| AM |
| AN |
∵AB=1.6m，EF=2m，BD=27m，FD=24m，
∴
| 2-1.6 |
| CN |
| 27-24 |
| 27 |
解得：CN=3.6m，
则树的高度为3.6+1.6=5.2m．
练习册系列答案
相关题目
在点A处向窗外的公路望去．