题目内容
如图,在等腰梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() 分别是
分别是![]() 的中点,
的中点,![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若四边形![]() 是正方形,请探索等腰梯形
是正方形,请探索等腰梯形![]() 的高和底边
的高和底边![]() 的数量关系,并
的数量关系,并![]() 证明你的结论.
证明你的结论.
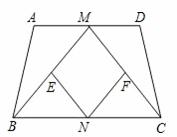
![]()
(1)证明:∵ 四边形![]() 为等腰梯形,∴
为等腰梯形,∴![]() ,∠
,∠![]() ∠
∠![]() .
.
∵![]() 为
为![]() 的中点,∴
的中点,∴ ![]() . ∴ △
. ∴ △![]() ≌△
≌△![]() .∴
.∴ ![]() .
.
∵![]() 分别是
分别是![]() 的中点,∴
的中点,∴ ![]() 分别为△
分别为△![]() 的中位线,
的中位线,
∴ ![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
∴![]() .∴ 四边形
.∴ 四边形![]() 是菱形.
是菱形.
(2)解:结论:等腰梯形![]() 的高是底边
的高是底边![]() 的一半.
的一半.
理由:连接![]() ,
,
∵![]() ,
,![]() ,∴
,∴ ![]() .
.
∵ ![]() ∥
∥![]() ,∴
,∴ ![]() .∴
.∴ ![]() 是梯形
是梯形![]() 的高.
的高.
又∵ 四边形![]() 是正方形,∴ △
是正方形,∴ △![]() 为直角三角形.
为直角三角形.
又∵![]() 是
是![]() 的中点,∴
的中点,∴ ![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
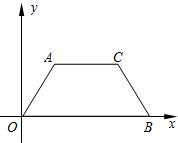 ,B(8,0).
,B(8,0). 中,
中, ,
, ,
, ,
, =
= .直角三角板含
.直角三角板含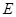 在边
在边 上移动,一直角边始终经过点
上移动,一直角边始终经过点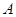 ,斜边与
,斜边与 交于点
交于点 .若
.若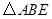 为等腰三角形,则
为等腰三角形,则 的长等于 .
的长等于 . 
 中,
中, ∥
∥ ,AD=AB.过
,AD=AB.过 作
作 ,交
,交 ,延长
,延长 ,使
,使 .
.
 的形状,并证明;
的形状,并证明; ,
, ,求三角形
,求三角形 的面积.
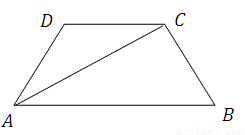
的面积.  中,
中, ,
, ,
, ,
, ,
, ,则上底
,则上底 的长是_______
的长是_______ .
.
 中,
中, ∥
∥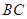 ,已知
,已知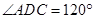 ,
,
 的度数;
的度数; ,
, ,试求等腰梯形
,试求等腰梯形