题目内容
 已知:如图,△ABC是等边三角形,BD是AC边上的中线,
已知:如图,△ABC是等边三角形,BD是AC边上的中线,延长BC到E,使CE=CD,
(1)(4分)不添加任何辅助线的情况下,请你至少写出两个与CD有关且形式不同的结论;
(2)(6分)问:BD=DE成立吗?若成立,请你写出相应的理由.
分析:(1)由BD是AC边上的中线,可得CD=
AC,又△ABC是等边三角形,CE=CD,所以CD=CE=
BC,从而得出CD=
BE;
(2)欲证BD=DE,只需证∠DBE=∠E,根据等边三角形的性质及角的等量关系可证明∠DBE=∠E=30°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)欲证BD=DE,只需证∠DBE=∠E,根据等边三角形的性质及角的等量关系可证明∠DBE=∠E=30°.
解答:解:(1)∵由BD是AC边上的中线,
∴CD=
AC;
又△ABC是等边三角形,CE=CD,
∴CD=CE=
BC,
∴BC=2CD,
∴2CD+CD=BE,
CD=
BE;
即与CD有关且形式不同的结论为:CD=
AC,CD=
BE;
(2)BD=DE成立,
∵△ABC为等边三角形,BD是AC边的中线,
∴BD⊥AC,BD平分∠ABC,∠DBE=12∠ABC=30°.
∵CD=CE,
∴∠CDE=∠E.
∵∠ACB=60°,且∠ACB为△CDE的外角,
∴∠CDE+∠E=60°.
∴∠CDE=∠E=30°,
∴∠DBE=∠DEB=30°,
∴BD=DE.
∴CD=
| 1 |
| 2 |
又△ABC是等边三角形,CE=CD,
∴CD=CE=
| 1 |
| 2 |
∴BC=2CD,
∴2CD+CD=BE,
CD=
| 1 |
| 3 |
即与CD有关且形式不同的结论为:CD=
| 1 |
| 2 |
| 1 |
| 3 |
(2)BD=DE成立,
∵△ABC为等边三角形,BD是AC边的中线,
∴BD⊥AC,BD平分∠ABC,∠DBE=12∠ABC=30°.
∵CD=CE,
∴∠CDE=∠E.
∵∠ACB=60°,且∠ACB为△CDE的外角,
∴∠CDE+∠E=60°.
∴∠CDE=∠E=30°,
∴∠DBE=∠DEB=30°,
∴BD=DE.
点评:本题考查等腰三角形与等边三角形的性质及三角形内角和为180°等知识.此类已知三角形边之间的关系求角的度数的题,一般是利用等腰(等边)三角形的性质得出有关角的度数,进而求出所求角的度数.

练习册系列答案
相关题目
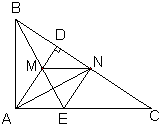 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.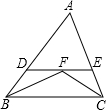 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.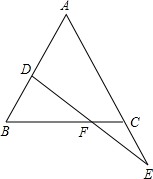 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.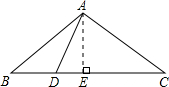 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.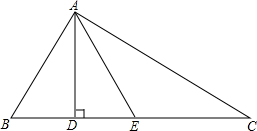 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.