题目内容
【题目】如图所示是二次函数y=ax2+bx+c（a≠0）图象的一部分，图象过点A（3，0），二次函数图象对称轴为直线x=1，给出四个结论：①b2＞4ac；②bc＜0；③2a+b=0；④当y＞0时，0＜x＜3．其中正确的结论有（ ）
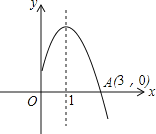
A. 2个 B. 3个 C. 4个 D. 1个
【答案】A
【解析】根据抛物线与x轴的交点个数可判断b24ac＞0，即b2＞4ac；根据抛物线对称轴为x＝
＝1，由a＜0得到b＞0，且2a＋b＝0，再利用抛物线与y轴的交点在x轴上方得到c＞0，可判断bc＞0；由于抛物线与x轴交于点A（3，0），得到抛物线与x轴的另一个交点为（1，0），所以当1＜x＜3时，y＞0．
∵抛物线与x轴有两个交点，
∴b24ac＞0，即b2＞4ac，所以①正确；
∵抛物线开口向下，
∴a＜0，
∵抛物线对称轴为x＝＝1，
∴b＞0，2a＋b＝0，所以③正确；
∵抛物线与y轴的交点在x轴上方，
∴c＞0，
∴bc＞0，所以②错误；
∵抛物线与x轴交于点A（3，0），对称轴为直线x＝1，
∴抛物线与x轴的另一个交点为（1，0），
∴当1＜x＜3时，y＞0，所以④错误．
故选：A
浙江名校名师金卷系列答案
【题目】泉州市某校准备组织教师、学生、家长到福州进行参观学习活动，旅行社代办购买动车票，动车票价格如下表所示：
运行区间 | 大人票价 | 学生票 | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
泉州 | 福州 | 65（元） | 54（元） | 40（元） |
根据报名总人数，若所有人员都买一等座的动车票，则共需13650元，若都买二等座动车票（学生全部按表中的“学生票二等座”购买），则共需8820元；已知家长的人数是教师的人数的2倍．
（1）设参加活动的老师有m人，请直接用含m的代数式表示教师和家长购买动车票所需的总费用；
（2）求参加活动的总人数；
（3）如果二等座动车票共买到x张，且学生全部按表中的“学生票二等座”购买 ，其余的买一等座动车票，且买票的总费用不低于9000元，求x的最大值．
