Question

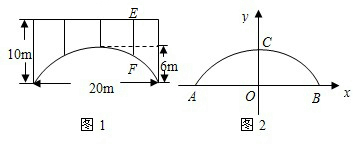
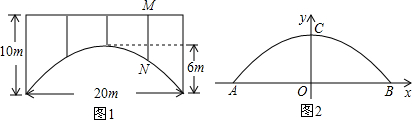
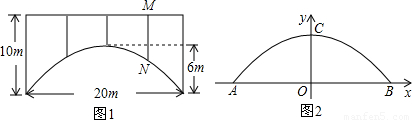
一座拱桥的轮廓是抛物线型（如图1所示），拱高6m，跨度20m，相邻两支柱间的距离均为5m．

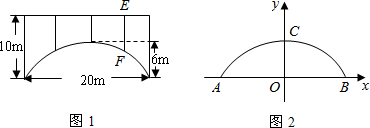
（1）将抛物线放在所给的直角坐标系中（如图2所示），求抛物线的表达式；
（2）求支柱EF的长度．

Answer 1

分析：（1）根据题目可知A，B，C的坐标，设出抛物线的解析式代入可求解．
（2）设F点的坐标为（5，y_F）可求出支柱MN的长度．

解答：解：（1）根据题目条件A，B，C的坐标分别是（-10，0），（10，0），（0，6），
设抛物线的解析式为y=ax²+c，
将B，C的坐标代入y=ax²+c，
得

6=c 0=100a+c

，
解得

a=- 3 50 c=6

．
所以抛物线的表达式y=-

3

50

x²+6．

（2）可设F（5，y_F），于是
y_F=-

3

50

×5²+6=4.5
从而支柱EF的长度是10-4.5=5.5米．

点评：此题主要考查了点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．