题目内容
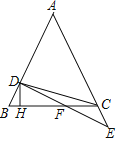
【题目】如图,在△ABC中,AB=AC,点D在AB上,点E在AC延长线上,且BD=CE,连接DE交BC于点F,作DH⊥BC于点H,连接CD.若tan∠DFH=![]() ,S△BCD=18,则DE的长为_____.
,S△BCD=18,则DE的长为_____.
【答案】6![]()
【解析】
如图,作EJ⊥BC交BC的延长线于J.利用全等三角形的性质证明DH=DJ,FH=FJ,BC=HJ=2FH,设DH=m,FH=2m,构建方程即可解决问题.
解:如图,作EJ⊥BC交BC的延长线于J.

∵AB=AC,
∴∠B=∠ACB=∠ECJ,
∵BD=EC,∠DHB=∠J=90°,
∴△DHB≌△EJC(AAS),
∴DH=EJ,BH=CJ,
∴BC=HJ,
∵∠DHF=∠J=90°,∠DFH=∠EFJ,
∴△DHF≌△EJF(AAS),
∴BC=HJ=2FH,DF=EF,
∵tan∠DFH=![]() =
=![]() ,
,
∴可以假设DH=m,FH=2m,则CB=4m,
∵S△BCD=18,
∴![]() ×4m×m=18,
×4m×m=18,
∴m=3或﹣3(舍弃),
∴DH=3,FH=6,
∴DF=EF=![]() =
=![]() =
=![]() ,
,
∴DE=2DF=![]() ,
,
故答案为:6![]() .
.

练习册系列答案
相关题目
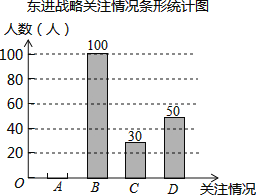
【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | n |
D.不知道 | 50 | 0.25 |
(1)根据上述统计图可得此次采访的人数为 人,m= ,n= ;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有 人.