题目内容
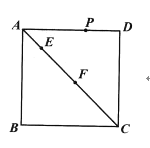
【题目】如图,在△ABC中,∠C=90°,D为AC上的一点,过D作DE⊥AC,过B作BE⊥AB,DE,BE交于点 E.已知BC=3,AB=5.
(1)证明:△EFB∽△ABC.
(2)若CD=1,请求出ED的长.
(3)连结AE,记CD=a,△AFE与△EBF面积的差为b.若存在实数t1,t2,m(其中t1≠t2),当a=t1或a=t2时,b的值都为m.求实数m的取值范围.

【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据相似三角形的判定定理,可求证.(2)过点B作BG⊥ED于G,可得四边形BGDC是矩形,进而可得△EBG∽△ABC,从而求得ED的长.(3)根据△EBG∽△ABC,可得BE,再根据DE∥BC,可得△AFD∽△ABC,即得到AF,从而得到m的取值范围.
解:(1)∵DE⊥AC,BE⊥AB,∠C=90°,
∴DE∥BC,∠EBF=∠ACB=90°,
∴∠EFB=∠ABC,
∴△EFB∽△ABC;
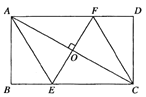
(2)如图,过点B作BG⊥ED于G,

则∠BGE=∠BGD=∠EDC=∠C=90°,
∴四边形BGDC是矩形,
∴BG=CD=1,BC=GD=3,
∵△EFB∽△ABC,
∴∠BEF=∠CAB,
∴△EBG∽△ABC,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
则![]() ;
;
(3)∵CD=a,AC=4,
∴BG=a,AD=4﹣a,
∵△EBG∽△ABC,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∵DE∥BC,
∴△AFD∽△ABC,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
则![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
∴m的取值范围是![]() .
.

【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?