题目内容
下列说法正确的是（ ）
分析：根据全等三角形的判定定理进行判断．
解答：解：A、两边和其中一边的对角对应相等的两个三角形不一定全等，根据SSA并不能证明三角形全等，故本选项错误；
B、如果相等的这条边是其中一个三角形的直角边，而是另一个三角形的斜边时，有一条边和一个锐角对应相等的两个直角三角形不全等，故本选项错误；
C、有两个角和一条边对应相等的两个三角形根据AAS或者ASA可以证得它们全等，故本选项正确；
D、有两条边对应相等的两个直角三角形不一定全等，例如，一直角三角形的斜边与另一直角三角形的斜边对应相等时，这两个直角三角形不全等，故本选项错误；
故选：C．
B、如果相等的这条边是其中一个三角形的直角边，而是另一个三角形的斜边时，有一条边和一个锐角对应相等的两个直角三角形不全等，故本选项错误；
C、有两个角和一条边对应相等的两个三角形根据AAS或者ASA可以证得它们全等，故本选项正确；
D、有两条边对应相等的两个直角三角形不一定全等，例如，一直角三角形的斜边与另一直角三角形的斜边对应相等时，这两个直角三角形不全等，故本选项错误；
故选：C．
点评：此题主要考查了三角形全等的条件，一般两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，但AAA、SSA，无法证明三角形全等．
练习册系列答案
相关题目
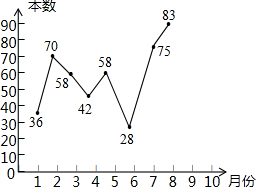（2012•东莞模拟）某班去年1～8月“书香校园”活动中全班同学的课外阅读量（单位：本），绘制了如图折线统计图，下列说法正确的是（ ）
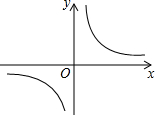（2013•葫芦岛）如图是反比例函数y=