题目内容
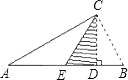
【题目】如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于______度.
【答案】30
【解析】据直角三角形斜边上的中线等于斜边的一半可得到AC=AE,从而得到∠A=∠ACE,再由折叠的性质及三角形的外角性质得到∠B=2∠A,从而不难求得∠A的度数.
解:∵在Rt△ABC中,CE是斜边AB的中线,
∴AE=CE,
∴∠A=∠ACE,
∵△CED是由△CBD折叠而成,
∴∠B=∠CED,
∵∠CEB=∠A+∠ACE=2∠A,
∴∠B=2∠A,
∵∠A+∠B=90°,
∴∠A=30°.
故答案为:30.
考查:(1)在直角三角形中,斜边上的中线等于斜边的一半;(2)三角形的外角性质:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c中x和y的值如下表:( )
x | 0.10 | 0.11 | 0.12 | 0.13 | 0.14 |
y | -5.6 | -3.1 | -1.5 | 0.9 | 1.8 |
则ax2+bx+c=0的一个根的范围是( )
A.0.10<x<0.11B.0.11<x<0.12C.0.12<x<0.13D.0.13<x<0.14