题目内容
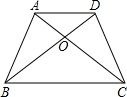
如图,四边形ABCD中,AD∥BC,AC与BD相交于点O,
(1)△ABC与△DBC的面积相等吗?为什么?
(2)若S△AOB=21cm2,求S△COD;
(3)若S△AOD=10cm2,且BO:OD=2:1,求S△ABD.
(1)△ABC与△DBC的面积相等吗?为什么?
(2)若S△AOB=21cm2,求S△COD;
(3)若S△AOD=10cm2,且BO:OD=2:1,求S△ABD.

(1))△ABC与△DBC的面积相等,理由是:
∵AD∥BC,
∴△ABC的边BC上的高和△DBC边BC上的高相等,设此高为h,
∴△ABC的面积是
BC×h,△DBC的面积是
×BC×h,
∵BC=BC,
∴△ABC与△DBC的面积相等;
(2)∵S△ABC=S△DBC,
∴S△ABC-S△OBC=S△DBC-S△OBC,
∴S△AOB=S△DOC=21cm2,
即S△COD=21cm2;
(3)∵BO:OD=2:1,
∴BD=3OD,
∵△AOD的边OD上的高和△ABD的边BD上的高相等,设此高为a,
∵S△AOD=
×OD×a=10cm2,
∴S△ABD.=
×BD×a=
×3OD×a=3×10cm2=30cm2.
∵AD∥BC,
∴△ABC的边BC上的高和△DBC边BC上的高相等,设此高为h,
∴△ABC的面积是
| 1 |
| 2 |
| 1 |
| 2 |
∵BC=BC,
∴△ABC与△DBC的面积相等;
(2)∵S△ABC=S△DBC,
∴S△ABC-S△OBC=S△DBC-S△OBC,
∴S△AOB=S△DOC=21cm2,
即S△COD=21cm2;
(3)∵BO:OD=2:1,
∴BD=3OD,
∵△AOD的边OD上的高和△ABD的边BD上的高相等,设此高为a,
∵S△AOD=
| 1 |
| 2 |
∴S△ABD.=
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目