题目内容
已知一元二次方程x2-4x+k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.
【答案】
(1)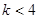 ;(2)0或
;(2)0或
【解析】
试题分析:(1)根据方程有两个不相等的实数根可得根的判别式△ ,即可得到关于k的不等式,解出即可;
,即可得到关于k的不等式,解出即可;
(2)先找出符合条件的最大整数k,即可求得一元二次方程x2-4x+k=0的解,再根据两个方程有一个相同的根,即可求得结果.
(1)∵方程有两个不相等的实数根,∴b2-4ac=16-4k>0,∴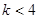 ;
;
(2)当k取最大整数时,即k=3,这时方程为x2-4x+3=0,∴x1=1,x2=3.
当相同根为x=1时,有1+m-1=0,m=0,
当相同根为x=3时,有9+3m-1=0,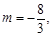
∴m的值是0或
考点:一元二次方程根的判别式,方程的解的定义
点评:解题的关键是熟记一元二次方程根的情况与判别式△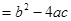 的关系:(1)
的关系:(1)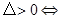 方程有两个不相等的实数根;(2)
方程有两个不相等的实数根;(2)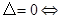 方程有两个相等的实数根;(3)
方程有两个相等的实数根;(3)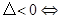 方程没有实数根.
方程没有实数根.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目