题目内容
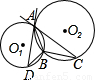
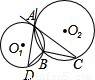
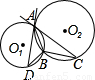
如图，A、B是圆O1和圆O2的公共点，AC是圆O1的切线，AD是圆O2的切线．若BC=4，AB=6，则BD的长为（ ）
| A．8 | B．9 | C．10 | D．12 |
∵AC是圆O1的切线，AD是圆O2的切线，
∴∠CAB=∠D，∠DAB=∠C，
∴△BAC∽△BDA，
∴
=
，
即AB2=BC?BD，
∵BC=4，AB=6，
∴BD=9．
故选B．
∴∠CAB=∠D，∠DAB=∠C，
∴△BAC∽△BDA，
∴
| BD |
| AB |
| AB |
| BC |
即AB2=BC?BD，
∵BC=4，AB=6，
∴BD=9．
故选B．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
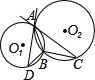如图，A、B是圆O1和圆O2的公共点，AC是圆O1的切线，AD是圆O2的切线．若BC=4，AB=6，则BD的长为（ ）| A、8 | B、9 | C、10 | D、12 |
