题目内容
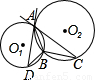
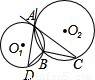
如图，A、B是圆O1和圆O2的公共点，AC是圆O1的切线，AD是圆O2的切线．若BC=4，AB=6，则BD的长为（ ）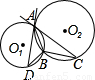
A．8
B．9
C．10
D．12
【答案】分析：CA，DA分别是两圆切线，由弦切勾股定理可知，∠CAB=∠D，∠DAB=∠C，故可判定△BAC∽△BDA，根据相似比可得AB2=BC•BD，代入BC=4，AB=6可解得BD的值．
解答：解：∵AC是圆O1的切线，AD是圆O2的切线，
∴∠CAB=∠D，∠DAB=∠C，
∴△BAC∽△BDA，
∴
=
，
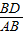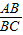即AB2=BC•BD，
∵BC=4，AB=6，
∴BD=9．
故选B．
点评：本题利用了弦切勾股定理，相似三角形的判定和性质求解．
解答：解：∵AC是圆O1的切线，AD是圆O2的切线，
∴∠CAB=∠D，∠DAB=∠C，
∴△BAC∽△BDA，
∴
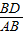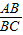=，即AB2=BC•BD，
∵BC=4，AB=6，
∴BD=9．
故选B．
点评：本题利用了弦切勾股定理，相似三角形的判定和性质求解．
练习册系列答案
阅读快车系列答案
相关题目
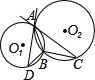如图，A、B是圆O1和圆O2的公共点，AC是圆O1的切线，AD是圆O2的切线．若BC=4，AB=6，则BD的长为（ ）| A、8 | B、9 | C、10 | D、12 |
