题目内容
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4) 、C(0,2).
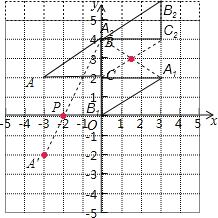
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4) ,画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.

【答案】(1)答案见解析;(2)旋转中心的坐标(![]() ,3);(3)点P(-2,0)
,3);(3)点P(-2,0)
【解析】
(1)根据网格结构找出点A、B以点C为旋转中心旋转180°的对应点A1、B1的位置,然后与点C顺次连接即可;再根据网格结构找出点A、B、C平移后的对应点A2、B2、C2的位置,然后顺次连接即可;
(2)根据中心对称的性质,连接两对对应顶点,交点即为旋转中心,然后写出坐标即可;
(3)根据轴对称确定最短路线问题,找出点A关于x轴的对称点A′的位置,然后连接A′B与x轴的交点即为点P.
解:(1)△A1B1C如图所示,
△A2B2C2如图所示;
(2)如图,旋转中心坐标为(![]() ,3);
,3);
(3)如图所示,点P的坐标为(-2,0).

练习册系列答案
相关题目
【题目】某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:千帕)随气体体积V(单位:立方米)的变化而变化,P随V的变化情况如下表所示.
P | 1.5 | 2 | 2.5 | 3 | 4 | … |
V | 64 | 48 | 38.4 | 32 | 24 | … |
(1)写出符合表格数据的P关于V的函数表达式 ;
(2)当气球的体积为20立方米时,气球内气体的气压P为多少千帕?
(3)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数表达式,基于安全考虑,气球的体积至少为多少立方米?