题目内容
【题目】某校学生准备购买标价为50元的《现代汉语词典》,现有甲、乙两书店出售此书,甲店按如下方法促销:若只购1本,则按原价销售;若一次性购买多于1本,但不多于30本时,每多购一本,售价在标价的基础上优惠2%(例如买2本,每本售价优惠2%;买三本,每本售价优惠4%,以此类推);若多于30本,每本售价20元.乙书店一律按标价的6折销售.
(1)分别写出在两书店购买此书总价y甲、y乙与购书本数x之间的函数关系式;
(2)若这些学生一次性购买多于30本时,那么去哪家书店购买更划算,为什么?若要一次性购买不多于30本时,先写出y(y=y甲﹣y乙)与购买本数x之间的函数式,画出其图象,再利用函数图象分析去哪家书店购买更划算.
【答案】(1)y甲=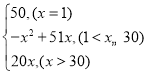 ,y乙=30x;(2)大于30本时到甲书店购买更合算;y=
,y乙=30x;(2)大于30本时到甲书店购买更合算;y=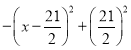 ,若购书少于21本,则到乙书店购买更合算;若购书21本,到甲,乙购书的费用一样;若购书超过21本但不多于30本,则到甲书店购书更合算.图象见解析.
,若购书少于21本,则到乙书店购买更合算;若购书21本,到甲,乙购书的费用一样;若购书超过21本但不多于30本,则到甲书店购书更合算.图象见解析.
【解析】
(1)分别根据两个书店购书的优惠方案得出y与x的函数关系式即可;
(2)首先得出y与x的函数关系式,进而画出图象,利用图象分析得出答案.
解:(1)设购买x本,当x=1时,y甲=50;当![]() 时,
时,![]() ;当x>30时,y甲=20x.
;当x>30时,y甲=20x.
故在甲书店购书的总费用为:
y甲=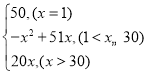 ,
,
在乙书店购书的总费用为:y乙=50×0.6x=30x;
(2)当x>30时,显然y甲<y乙,即到甲书店购买更合算,
当1<x≤30时,y=y甲﹣y乙=﹣x2+51x﹣30x=﹣x2+21x=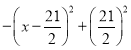 ,
,
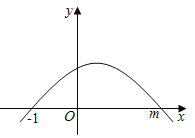
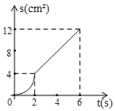
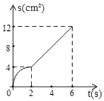
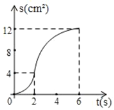
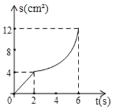
当﹣x2+21x=0时,解得:x1=0,x2=21,故函数图象如下:
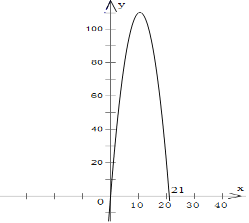
由图象可得出:当1<x<21时,y>0,
当x=21时,y=0,
当30>x>21时,y<0,
综上所述,若购书少于21本,则到乙书店购买更合算;若购书21本,到甲,乙购书的费用一样;若购书超过21但不多于30本,则到甲书店购书更合算.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案