题目内容
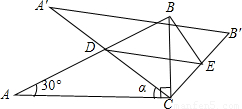
(2010•龙岩质检)如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C顺时针旋转α角(0°<α<90°),得到Rt△A′B′C,A′C与AB交于点D,过点D作DE∥A′B′交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.(1)当α=30°时,求x的值.
(2)求S与x的函数关系式,并写出x的取值范围;
(3)以点E为圆心,BE为半径作⊙E,当S=
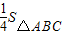 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.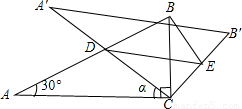
【答案】分析:(1)根据等腰三角形的判定,∠A=∠α=30°,得出x=1;
(2)由直角三角形的性质,AB=2,AC=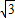 ,由旋转性质求得△ADC∽△BCE,根据比例关系式,求出S与x的函数关系式;
,由旋转性质求得△ADC∽△BCE,根据比例关系式,求出S与x的函数关系式;
(3)当S=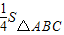 时,求得x的值,判断⊙E和DE的长度大小,确定⊙E与A′C的位置关系,再求tanα值.
时,求得x的值,判断⊙E和DE的长度大小,确定⊙E与A′C的位置关系,再求tanα值.
解答: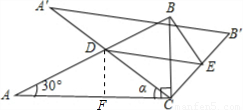 解:(1)∵∠A=a=30°,
解:(1)∵∠A=a=30°,
又∵∠ACB=90°,
∴∠ABC=∠BCD=60°.
∴AD=BD=BC=1.
∴x=1;
(2)∵∠DBE=90°,∠ABC=60°,
∴∠A=∠CBE=30°.
∴AC=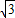 BC=
BC= ,AB=2BC=2.
,AB=2BC=2.
由旋转性质可知:AC=A′C,BC=B′C,
∠ACD=∠BCE,
∴△ADC∽△BEC,
∴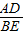 =
= ,
,
∴BE=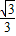 x.
x.
∵BD=2-x,
∴s= ×
×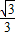 x(2-x)=-
x(2-x)=- x2+
x2+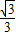 x.(0<x<2)
x.(0<x<2)
(3)∵s= s△ABC
s△ABC
∴-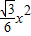 +
+ =
=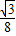 ,
,
∴4x2-8x+3=0,
∴ ,
, .
.
①当x= 时,BD=2-
时,BD=2- =
= ,BE=
,BE= ×
× =
=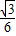 .
.
∴DE=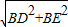 =
= .
.
∵DE∥A′B′,
∴∠EDC=∠A′=∠A=30°.
∴EC= DE=
DE=
 >BE,
>BE,
∴此时⊙E与A′C相离.
 过D作DF⊥AC于F,则
过D作DF⊥AC于F,则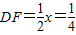 ,
,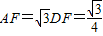 .
.
∴ .
.
∴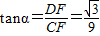 . (12分)
. (12分)
②当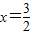 时,
时,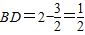 ,
,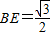 .
.
∴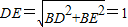 ,
,
∴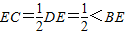 ,
,
∴此时⊙E与A'C相交.
同理可求出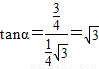 .
.
点评:本题考查的知识点:等腰三角形的判定,直角三角形的性质,相似三角形的判定以及直线与圆的位置关系的确定,是一道综合性较强的题目,难度大.
(2)由直角三角形的性质,AB=2,AC=
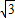 ,由旋转性质求得△ADC∽△BCE,根据比例关系式,求出S与x的函数关系式;
,由旋转性质求得△ADC∽△BCE,根据比例关系式,求出S与x的函数关系式;(3)当S=
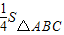 时,求得x的值,判断⊙E和DE的长度大小,确定⊙E与A′C的位置关系,再求tanα值.
时,求得x的值,判断⊙E和DE的长度大小,确定⊙E与A′C的位置关系,再求tanα值.解答:
 解:(1)∵∠A=a=30°,
解:(1)∵∠A=a=30°,又∵∠ACB=90°,
∴∠ABC=∠BCD=60°.
∴AD=BD=BC=1.
∴x=1;
(2)∵∠DBE=90°,∠ABC=60°,
∴∠A=∠CBE=30°.
∴AC=
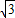 BC=
BC= ,AB=2BC=2.
,AB=2BC=2.由旋转性质可知:AC=A′C,BC=B′C,
∠ACD=∠BCE,
∴△ADC∽△BEC,
∴
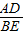 =
= ,
,∴BE=
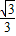 x.
x.∵BD=2-x,
∴s=
 ×
×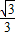 x(2-x)=-
x(2-x)=- x2+
x2+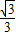 x.(0<x<2)
x.(0<x<2)(3)∵s=
 s△ABC
s△ABC∴-
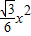 +
+ =
=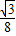 ,
,∴4x2-8x+3=0,
∴
 ,
, .
.①当x=
 时,BD=2-
时,BD=2- =
= ,BE=
,BE= ×
× =
=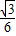 .
.∴DE=
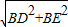 =
= .
.∵DE∥A′B′,
∴∠EDC=∠A′=∠A=30°.
∴EC=
 DE=
DE=
 >BE,
>BE,∴此时⊙E与A′C相离.
 过D作DF⊥AC于F,则
过D作DF⊥AC于F,则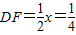 ,
,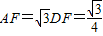 .
.∴
 .
.∴
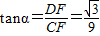 . (12分)
. (12分)②当
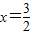 时,
时,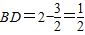 ,
,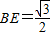 .
.∴
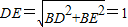 ,
,∴
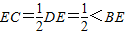 ,
,∴此时⊙E与A'C相交.
同理可求出
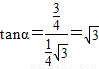 .
.点评:本题考查的知识点:等腰三角形的判定,直角三角形的性质,相似三角形的判定以及直线与圆的位置关系的确定,是一道综合性较强的题目,难度大.

练习册系列答案
相关题目