题目内容
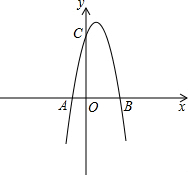 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8),
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8),(1)试求抛物线的解析式;
(2)设点D是该抛物线的顶点,试求直线CD的解析式;
(3)若直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴上、下平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
分析:(1)设出交点式,把点C坐标代入即可求解;
(2)设出直线解析式,把C,D两点坐标代入即可求解;
(3)向上平移时,把点E,F坐标代入设出的函数解析式求得最大范围即可;向下平移时,设出相应的二次函数解析式,与直线解析式组成方程组,让判别式为非负数求值即可.
(2)设出直线解析式,把C,D两点坐标代入即可求解;
(3)向上平移时,把点E,F坐标代入设出的函数解析式求得最大范围即可;向下平移时,设出相应的二次函数解析式,与直线解析式组成方程组,让判别式为非负数求值即可.
解答:解:(1)抛物线的解析式为y=a(x+2)(x-4),
∵抛物线与y轴交于点C(0,8),
∴-8a=8,解得a=-1,
∴y=-x2+2x+8;
(2)∵y=-x2+2x+8,
∴顶点坐标为(1,9),
设过CD的解析式为y=kx+b,
∴b=8,k+8=9,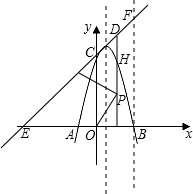
解得k=1,
∴过CD的解析式为y=x+8;
若直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴上、下平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
(3)由上求得E(-8,0),F(4,12).
①若抛物线向上平移,可设解析式为y=-x2+2x+8+m(m>0).
当x=-8时,y=-72+m.
当x=4时,y=m.
∴-72+m≤0或m≤12.
∴0<m≤72.
②若抛物线向下移,可设解析式为y=-x2+2x+8-m(m>0).
由
,
有x2-x+m=0.
∴△=1-4m≥0,
∴0<m≤
.
∴向上最多可平移72个单位长,向下最多可平移
个单位长.
∵抛物线与y轴交于点C(0,8),
∴-8a=8,解得a=-1,
∴y=-x2+2x+8;
(2)∵y=-x2+2x+8,
∴顶点坐标为(1,9),
设过CD的解析式为y=kx+b,
∴b=8,k+8=9,

解得k=1,
∴过CD的解析式为y=x+8;
若直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴上、下平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
(3)由上求得E(-8,0),F(4,12).
①若抛物线向上平移,可设解析式为y=-x2+2x+8+m(m>0).
当x=-8时,y=-72+m.
当x=4时,y=m.
∴-72+m≤0或m≤12.
∴0<m≤72.
②若抛物线向下移,可设解析式为y=-x2+2x+8-m(m>0).
由
|
有x2-x+m=0.
∴△=1-4m≥0,
∴0<m≤
| 1 |
| 4 |
∴向上最多可平移72个单位长,向下最多可平移
| 1 |
| 4 |
点评:过抛物线的三点里面有2个是与x轴的交点时,设出交点式计算比较简便;抛物线上下平移只改变常数项.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
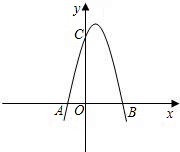 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).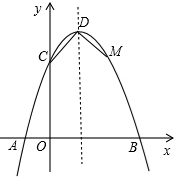 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1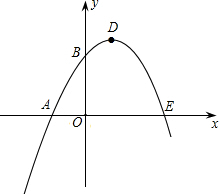 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )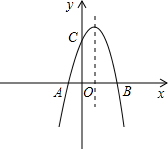 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).