题目内容
（2012•奉贤区二模）梯形ABCD中，AB∥CD，E、F是AD、BC的中点，若
=
，
=
，那么用
、
的线性组合表示向量
=
（
-
）
（
-
）．
| AB |
| a |
| CD |
| b |
| a |
| b |
| EF |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
分析：由梯形ABCD中，AB∥CD，E、F是AD、BC的中点，即可得EF是梯形ABCD的中位线，根据梯形中位线的性质，可得EF∥AB∥CD，EF=
（AB+CD），又由
=
，
=
，即可求得答案．
| 1 |
| 2 |
| AB |
| a |
| CD |
| b |
解答：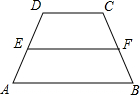
解：∵梯形ABCD中，AB∥CD，E、F是AD、BC的中点，
∴EF是梯形ABCD的中位线，
∴EF∥AB∥CD，EF=
（AB+CD），
∵
=
，
=
，
∴
=-
∴
=
（
-
）．
故答案为：
（
-
）．
解：∵梯形ABCD中，AB∥CD，E、F是AD、BC的中点，∴EF是梯形ABCD的中位线，
∴EF∥AB∥CD，EF=
| 1 |
| 2 |
∵
| AB |
| a |
| CD |
| b |
∴
| DC |
| b |
∴
| EF |
| 1 |
| 2 |
| a |
| b |
故答案为：
| 1 |
| 2 |
| a |
| b |
点评：此题考查了梯形中位线的性质与平面向量的知识．此题难度不大，注意掌握平行向量间的关系，注意数形结合思想的应用．
练习册系列答案
相关题目
（2012•奉贤区二模）已知长方体ABCD-EFGH如图所示，那么下列直线中与直线AB不平行也不垂直的直线是（ ）
