题目内容
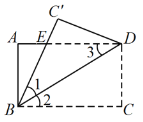
【题目】将一副三角板的直角重合放置,如图1所示,
(1)图1中∠BED的度数为 ;
(2)三角板△AOB的位置保持不动,将三角板△COD绕其直角顶点O顺时针方向旋转:
①当旋转至图2所示位置时,恰好OD∥AB,求此时∠AOC的大小;
②若将三角板△COD继续绕O旋转,直至回到图1位置,在这一过程中,是否会存在△COD其中一边能与AB平行?如果存在,请你画出图形,并直接写出相应的∠AOC的大小;如果不存在,请说明理由.

【答案】(1)15°;(2)①30°;②120°,165°,30°,150°,60°,15°.
【解析】
(1)根据三角形的外角性质和对顶角的性质求出∠BED的度数;
(2)①由OD∥AB可得∠BOD=∠B=30°,再由∠BOD+∠BOC=90°和∠AOC+∠BOC=90°求出∠AOC的度数;②根据题意作图,可分6种情况进行分析求解.
(1)∵∠CEA=∠BAO-∠C=60°-45°=15°,
∴∠BED=∠CEA=15°,
(2)①∵OD∥AB,
∴∠BOD=∠B=30°
又∠BOD+∠BOC=90°和∠AOC+∠BOC=90°
∴∠AOC=∠BOD=30°;
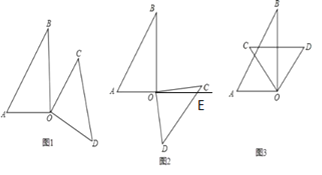
②存在,如图1,∵AB∥CO,
∴∠AOC=∠AOB+∠BOC=∠AOB+∠B=120°;
如图2,延长AO交CD于E,
∵AB∥DC,∴∠DEO=∠A=60°,又∠C=45°,∴∠COE=∠DEO-∠C=15°,
∴∠AOC=180°-∠COE=165°;
如图3,∵AB∥DO,
∴∠A+∠AOD=180°,
∵∠A=60°
∴∠AOD=120°
∴∠AOC=∠AOD-∠COD=30°;
如图4,∵AB∥DO,∴∠AOC=∠AOD+∠COD=∠BAO+∠COD=60°+90°=150°
如图5,∵AB∥CO,∴∠AOC=∠BAO =60°
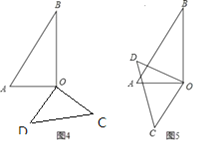
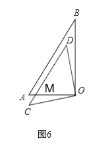
如图6,
设AO与CD相交于点M
∵AB∥CD,
∴∠DMO=∠A=60°
∴∠AOD=180°-45°-60°=75°,
∴∠AOC=90°-∠AOD =15°.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案