题目内容
(本题12分)如图甲,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.

小题1:(1)在图甲中,你发现线段AC、BD的数量关系是_______,直线AC、BD相交成____度角;
小题2:(2)将图甲中的 绕点O顺时针旋转
绕点O顺时针旋转 ,在图乙中作出旋转后的
,在图乙中作出旋转后的 ;
;
小题3:(3)将图甲中的 绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若
绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若 绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.
绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.

小题1:(1)在图甲中,你发现线段AC、BD的数量关系是_______,直线AC、BD相交成____度角;
小题2:(2)将图甲中的
 绕点O顺时针旋转
绕点O顺时针旋转 ,在图乙中作出旋转后的
,在图乙中作出旋转后的 ;
;小题3:(3)将图甲中的
 绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若
绕点O顺时针旋转一个锐角,得到图丙,这时(1)中的两个结论是否成立?作出判断,并说明理由.若 绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.
绕点O继续旋转更大的角度时,结论仍然成立吗?作出判断,不必说明理由.小题1:(1)AC=BD,

小题2:(2)略
小题3:(3)成立,证明略.结论仍然成立
分析:(1)的结论容易得到,AC=BD,AC与BD相交成90°的角;
(2)△OAB绕点O顺时针旋转90°角应该在△COD的右边;
(3)结论仍然成立,利用等腰直角三角形的性质可以得到全等条件证明△COA≌△DOB,然后利用全等三角形的性质可以证明结论仍然成立。
解答:
(1)在图1中,线段AC,BD的数量关系是相等,直线AC,BD相交成90度角;
(2)如图(a)[A,B字母位置互换扣分,无弧扣分,不连接AB扣分]
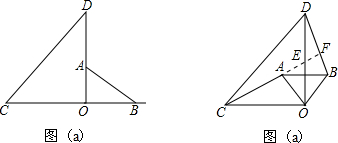
(3)成立,如右图
∵∠COD=∠AOB=90°,
∴∠COA+∠AOD=∠AOD+∠DOB,
即:∠COA=∠DOB(或由旋转得∠COA=∠DOB),
∵CO=OD,OA=OB,
∴△COA≌△DOB,
∴AC=BD,
延长CA交OD于E,交BD于F,(下面的证法较多)
∵△COA≌△DOB,
∴∠ACO=∠ODB,
∵∠CEO=∠DEF,
∴∠COE=∠EFD=90°,
∴AC⊥BD。
旋转更大角时,结论仍然成立。
点评:本题考查了图形的旋转变化,学生要看清是顺时针还是逆时针旋转,然后画出图形,利用图形的性质通过证明三角形全等就可以解决问题。

练习册系列答案
相关题目

 中,
中, ,
, ,将腰
,将腰 以
以 为旋转中心逆时针旋转90°至
为旋转中心逆时针旋转90°至 ,连接
,连接 的面积为3,则
的面积为3,则 的长为 ﹡
的长为 ﹡ 
 绕点
绕点 顺时针旋转
顺时针旋转 后得到
后得到 ,则
,则 点的对应点
点的对应点 的坐标是 ( )
的坐标是 ( )

 0并写出点A
0并写出点A ,B
,B

