题目内容
 如图,已知在梯形ABCD中,AD∥BC,点E、F、G分别在边AB、BC、CD上,四边形AEFG是平行四边形,AE=GC.
如图,已知在梯形ABCD中,AD∥BC,点E、F、G分别在边AB、BC、CD上,四边形AEFG是平行四边形,AE=GC.(1)求证:AB=DC;
(2)当∠FGC=2∠1时,试判断四边形AEFG的形状,并证明你的结论.
分析:(1)利用平行线的性质和判定以及平行四边形的性质得出,∠GFC=∠C,进而得出∠B=∠C即可得出答案;
(2)利用已知得出∠CGH=∠1,进而得出∠1+∠B=90°,求出∠BEF=90°,即∠AEF=90°,利用矩形的判定得出答案.
(2)利用已知得出∠CGH=∠1,进而得出∠1+∠B=90°,求出∠BEF=90°,即∠AEF=90°,利用矩形的判定得出答案.
解答: (1)证明:∵四边形AEFG是平行四边形,
(1)证明:∵四边形AEFG是平行四边形,
∴AE∥GF,AE=GF.
∴∠GFC=∠B.
∵AE=GC,AE=GF,∴GF=GC,∴∠GFC=∠C.
∴∠B=∠C.
∴AB=DC.
(2)解:四边形AEFG是矩形.
理由:作GH⊥BC于点H.
∵GF=GC,∴∠FGC=2∠CGH,
又∵∠FGC=2∠1,∴∠CGH=∠1,
∴∠CGH+∠C=90°,
∴∠1+∠B=90°,
∴∠BEF=90°,∴∠AEF=90°,
∴平行边形AEFG是矩形.
 (1)证明:∵四边形AEFG是平行四边形,
(1)证明:∵四边形AEFG是平行四边形,∴AE∥GF,AE=GF.
∴∠GFC=∠B.
∵AE=GC,AE=GF,∴GF=GC,∴∠GFC=∠C.
∴∠B=∠C.
∴AB=DC.
(2)解:四边形AEFG是矩形.
理由:作GH⊥BC于点H.
∵GF=GC,∴∠FGC=2∠CGH,
又∵∠FGC=2∠1,∴∠CGH=∠1,
∴∠CGH+∠C=90°,
∴∠1+∠B=90°,
∴∠BEF=90°,∴∠AEF=90°,
∴平行边形AEFG是矩形.
点评:此题主要考查了平行四边形的性质与矩形的判定定理和平行线的性质等知识,根据已知得出∠1+∠B=90°是解题关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
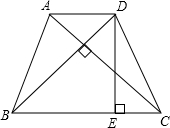 如图,已知在梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AC=6,则该梯形的高DE等于
如图,已知在梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AC=6,则该梯形的高DE等于 9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G. 27、如图,已知在梯形ABCD中,AD∥BC,AD+BC=CD,M是AB的中点,DM,CM是否分别是∠ADC和∠DCB的平分线?说明理由.
27、如图,已知在梯形ABCD中,AD∥BC,AD+BC=CD,M是AB的中点,DM,CM是否分别是∠ADC和∠DCB的平分线?说明理由.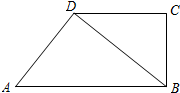 如图,已知在梯形ABCD中,AB∥CD,BC⊥AB,且AD⊥BD,CD=2,
如图,已知在梯形ABCD中,AB∥CD,BC⊥AB,且AD⊥BD,CD=2, 如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.
如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.