Question

【题目】学校科技小组研制了一套信号发射、接收系统.在对系统进行测试中，如图，小明从路口A处出发，沿东南方向笔直公路行进，并发射信号，小华同时从A处出发，沿西南方向笔直公路行进，并接收信号.若小明步行速度为39米／分，小华步行速度为52米／分，恰好在出发后30分时信号开始不清晰.

（1）你能求出他们研制的信号收发系统的信号传送半径吗？（以信号清晰为界限）

（2）通过计算，你能找到题中数据与勾股数3、4、5的联系吗？试从中寻找求解决问题的简便算法.

Answer 1

【答案】(1)1950米；(2)详见解析.

【解析】试题分析：

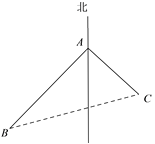
（1）设30分钟时，小明刚好到达C处，小华刚好到达B处，连接BC，则由已知易得AC=，AB=，∠BAC=90°，由勾股定理在Rt△ABC中计算出BC的长就可得收发系统的传送半径；

（2）由（1）可知：数据是一组勾股数，而，由此可知勾股数“3、4、5”的整数倍也是一组“勾股数”，这样我们就可以直接由“”来计算本题第（1）问中的传送半径了.

试题解析：

（1）如图，设30分钟时，小明刚好到达C处，小华刚好到达B处，连接BC，则由已知易得AC=，AB=，∠BAC=90°，

∴BC=（米），即信号传送半径为1950米；

（2）∵小明所走的路程为39×30＝3×13×30，小华所走的路程为52×30＝4×13×30，30分钟时，两人间的距离为： ，

∴结合（1）可知勾股数3、4、5的倍数仍能构成一组勾股数，

∴可用5×13×30=1950（米）来计算传送半径，这样比用勾股定理计算要简单一些.