题目内容
已知:如图,在平面直角坐标系中,O为坐标原点,B(5,0) ,M为等腰梯形OBCD底边OB上一点,OD=BC=2 ,∠DMC=∠DOB=60°。
(1) 求等腰梯形OBCD的周长;
(2) 求点M的坐标。
(1) 求等腰梯形OBCD的周长;
(2) 求点M的坐标。
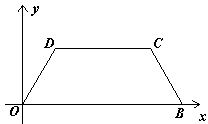
解:(1)过点D作DE⊥OB于E,过点C作CF⊥OB于F
∵四边形OBCD是等腰梯形,OD=BC
∴ Rt△ODE≌Rt△BCF ,四边形CDEF是矩形
∴ OE=BF ,DC=EF ∵ OD=BC=2, OB=5, ∠BOD=60°
∴ OE=BF=1 , DC=EF=3
∴ 梯形OBCD的周长是12
(2) 设点M的坐标为(x,0),联结DM和CM
∵ ∠BOD=∠CMD=∠OBC=60°
∴ ∠ODM+∠OMD=∠BMC+∠OMD=120°
∴ ∠ODM=∠BMC
∵ △OMD∽△BCM
∴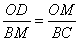 ∴
∴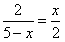
∴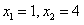
∴ 点M的坐标为(1, 0) 或(4,0)
∵四边形OBCD是等腰梯形,OD=BC
∴ Rt△ODE≌Rt△BCF ,四边形CDEF是矩形
∴ OE=BF ,DC=EF ∵ OD=BC=2, OB=5, ∠BOD=60°
∴ OE=BF=1 , DC=EF=3
∴ 梯形OBCD的周长是12
(2) 设点M的坐标为(x,0),联结DM和CM
∵ ∠BOD=∠CMD=∠OBC=60°
∴ ∠ODM+∠OMD=∠BMC+∠OMD=120°
∴ ∠ODM=∠BMC
∵ △OMD∽△BCM
∴
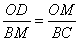 ∴
∴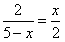
∴
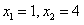
∴ 点M的坐标为(1, 0) 或(4,0)

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).

