题目内容
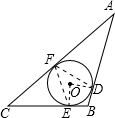已知三角形ABC的内切圆⊙O与AB、CB、AC分别相切于点D、E、F，若劣弧
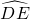的度数为80°，则下列结论错误的是
- A.∠DOE=80°
- B.∠DFE=40°
- C.∠ABC=100°
- D.∠ABC=140°
D
分析：根据弧的度数的定义，以及圆周角定理，切线的性质即可确定．
解答：∵劣弧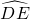的度数为80°
∴∠DOE=80°，故A正确；
∴∠DFE=
∠DOE=40°，故B正确；
∵AB，BC是圆的切线．
∴∠OEB=∠ODB=90°
∴∠ABC=360°-90°-90°-80°=100°，故C正确，D错误．
故选D．
点评：本题主要考查了三角形的内切圆，以及圆周角定理，正确理解定理是解题关键．
分析：根据弧的度数的定义，以及圆周角定理，切线的性质即可确定．
解答：∵劣弧
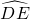的度数为80°∴∠DOE=80°，故A正确；
∴∠DFE=
∠DOE=40°，故B正确；∵AB，BC是圆的切线．
∴∠OEB=∠ODB=90°
∴∠ABC=360°-90°-90°-80°=100°，故C正确，D错误．
故选D．
点评：本题主要考查了三角形的内切圆，以及圆周角定理，正确理解定理是解题关键．
练习册系列答案
相关题目
已知三角形ABC是⊙O的内接三角形，∠BOC=140°，则∠BAC的度数为（ ）
| A、70° | B、110° | C、140° | D、70°或110° |
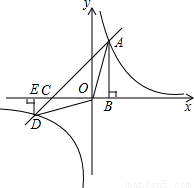
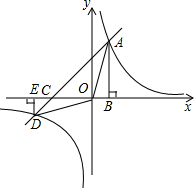内的交点，且S△AOB=3．
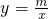的图象在第一象限
内的交点，且S△AOB=3．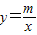
的图象在第一象限内的交点，且S△AOB=3．