题目内容
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,
求证:BP=2PQ.
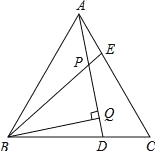
【答案】证明详见解析.
【解析】
试题分析:根据等边三角形的性质可得AB=AC,∠BAE=∠C=60°,再利用“边角边”证明△ABE和△CAD全等,根据全等三角形对应角相等可得∠1=∠2,然后求出∠BPQ=60°,再根据直角三角形两锐角互余求出∠PBQ=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半证明即可.
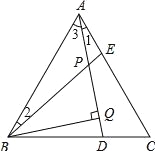
试题解析:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
AB=AC,∠BAE=∠C=60°,AE=CD,
∴△ABE≌△CAD(SAS),
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,
∵BQ⊥AD,
∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,
∴BP=2PQ.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目