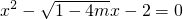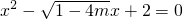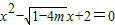Question

设方程有一个正根x₁，一个负根x₂，则以|x₁|、|x₂|为根的一元二次方程为（　　）

• A、x²-3x-m-2=0
• B、x²+3x-m-2=0
• C、x2-

  1-4m

  x-2=0
• D、x2-

  1-4m

  x+2=0

Answer 1

分析：根据一元二次方程根与系数的关系，可以写出两根和与两根积，然后由|x₁|+|x₂|＞0，|x₁|•|x₂|＞0进行判断作出选择．

解答：解：A∵|x₁|+|x₂|=3＞0，但|x₁|•|x₂|=-m-2不能确定它的正负，∴不能选A．
B∵|x₁|+|x₂|=-3＜0，∴不能选B．
C∵|x₁|+|x₂|=

1-4m

＞0，但|x₁|•|x₂|=-2＜0，∴不能选C．
D∵|x₁|+|x₂|=

1-4m

＞0，|x₁|•|x₂|=2＞0，∴选D．
故选D．

点评：本题考查的是一元二次方程根与系数的关系，根据根与系数的关系写出两根和与两根积，再由绝对值的意义确定选项．