题目内容
 如图所示,已知AB与CD相交于点F,BE平分∠CBF,DE平分∠ADC,试说明∠A、∠E、∠C三者之间的数量关系.
如图所示,已知AB与CD相交于点F,BE平分∠CBF,DE平分∠ADC,试说明∠A、∠E、∠C三者之间的数量关系.分析:连接EF并延长,根据三角形的一个外角等于与它不相邻的两个内角的和可以求出∠1+∠2+∠E=∠BFD,∠A+∠ADF=∠BFD,∠C+∠CBF=∠BFD,再根据角平分线的定义求出∠CBF=2∠1,∠ADF=2∠2,整理即可得解.
解答: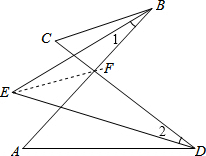 解:如图,连接EF并延长,
解:如图,连接EF并延长,
由三角形的外角性质,∠1+∠2+∠E=∠BFD,
∠A+∠ADF=∠BFD,
∠C+∠CBF=∠BFD,
∴∠A+∠ADF+∠C+∠CBF=2(∠1+∠2+∠E)=2∠1+2∠2+2∠E,
∵BE平分∠CBF,DE平分∠ADC,
∴∠CBF=2∠1,∠ADF=2∠2,
∴∠A+∠C=2∠E.
 解:如图,连接EF并延长,
解:如图,连接EF并延长,由三角形的外角性质,∠1+∠2+∠E=∠BFD,
∠A+∠ADF=∠BFD,
∠C+∠CBF=∠BFD,
∴∠A+∠ADF+∠C+∠CBF=2(∠1+∠2+∠E)=2∠1+2∠2+2∠E,
∵BE平分∠CBF,DE平分∠ADC,
∴∠CBF=2∠1,∠ADF=2∠2,
∴∠A+∠C=2∠E.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目

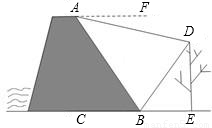
 角.在A处测得树顶D的俯角为15
角.在A处测得树顶D的俯角为15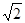 ≈1.4
≈1.4  ≈1.7)
≈1.7)
 角.在A处测得树顶D的俯角为15
角.在A处测得树顶D的俯角为15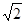 ≈1.4
≈1.4 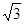 ≈1.7)
≈1.7)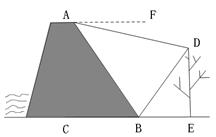
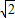 ≈1.4
≈1.4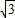 ≈1.7)
≈1.7)