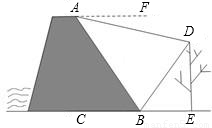
题目内容
星期天,小强去水库大坝游玩,他站在大坝上的A处看到一棵大树的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60 角.在A处测得树顶D的俯角为15
角.在A处测得树顶D的俯角为15 .如图所示,已知AB与地面的夹角为 60
.如图所示,已知AB与地面的夹角为 60 ,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据
,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据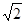 ≈1.4
≈1.4 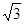 ≈1.7)
≈1.7)
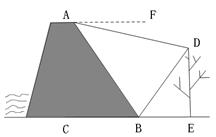
【答案】
∵AF∥CE,∠ABC=60°,
∴∠FAB=60°.
∵∠FAD=15°,
∴∠DAB=45°.
∵∠DBE=60°,∠ABC=60°,
∴∠ABD=60°.
过点D作DM⊥AB于点M,则有AM=DM.

∵tan∠ABD= ,
,
∴tan60°= ,
,
∴DM=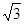 BM.
BM.
设BM=x,则AM=DM=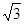 x.
x.
∵AB=AM+BM=8,
∴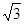 x+x=8,
x+x=8,
∴x=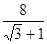 ≈3.0,
≈3.0,
∴DM=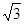 x≈5.
x≈5.
∵∠ABD=∠DBE=60°,DE⊥BE,DM⊥AB,
∴DE=DM≈5(米).
答:这棵树约有5米高.
【解析】利用题中所给的角的度数可得到△ABD中各角的度数,进而把已知线段AB整理到直角三角形中,利用相应的三角函数即可求得所求线段的长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 角.在A处测得树顶D的俯角为15
角.在A处测得树顶D的俯角为15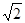 ≈1.4
≈1.4  ≈1.7)
≈1.7)
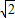 ≈1.4
≈1.4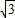 ≈1.7)
≈1.7)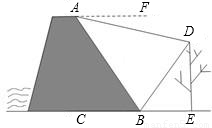
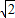 ≈1.4
≈1.4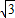 ≈1.7)
≈1.7)