题目内容
1、已知直线a,b,c,且a∥b,c与a相交,求证:c与b也相交.
分析:先假设c∥b,然后根据平行线的性质证得假设不成立,从而得出原结论成立.
解答:证明:假设c∥b;
∵a∥b,
∴c∥a,这与c和a相交相矛盾,假设不成立;
所以c与b也相交.
∵a∥b,
∴c∥a,这与c和a相交相矛盾,假设不成立;
所以c与b也相交.
点评:解此题关键要懂得反证法的意义及步骤.反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

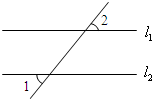 (2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2=
(2007•黔南州)如图,已知直线l1∥l2,∠1=50°,那么∠2= (2012•株洲模拟)如图,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,且∠OBA=40°,则∠ADC的度数为( )
(2012•株洲模拟)如图,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,且∠OBA=40°,则∠ADC的度数为( )
 如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=8,则AB、CD之间的距离为
如图,已知直线AB∥CD,直线EF截AB、CD于E、F,EG⊥CD,∠EFD=45°且FG=8,则AB、CD之间的距离为