Question

【题目】在平面直角坐标系中，O为坐标原点，A(m,n+1),B(m+2,n).

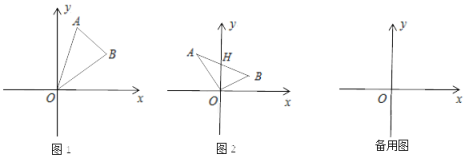
（1）当m=1,n=2时.如图1，连接AB、AO、BO.直接写出△ABO的面积为 .

（2）如图2，若点A在第二象限、点B在第一象限，连接AB、AO、BO,AB交y轴于H，△ABO的面积为2.求点H的坐标.

（3）若点A、B在第一象限，在y 轴正半轴上存在点C，使得∠CAB=900,且CA=AB,求m的值，及OC的长（用含n的式子表示）.

Answer 1

【答案】（1）；（2）点H的坐标（0，2）；（3）OC=n-1（n＞1），m=1

【解析】

（1）过点A作AC⊥y轴于点C，过点B作BD⊥x轴于点D，AC、BD交于点E，求出各点坐标，然后利用△ABO所在矩形的面积减去周围三角形的面积计算即可；

（2）根据计算即可；

（3）过点A作ADy轴，垂足为D，延长DA，过点B作BEDA，交DA的延长线于点E，首先证明，得到AD=BE=m，CD=AE=2，然后列式计算即可.

（1）如图，过点A作AC⊥y轴于点C，过点B作BD⊥x轴于点D，AC、BD交于点E，

∵m=1，n=2，

∴A(1，3),B(3，2)，

∴C（0，3），E（3，3），D（3，0），

∴S△ABO；

（2）==OH=2，

点H的坐标（0，2）；

（3）过点A作ADy轴，垂足为D，延长DA，过点B作BEDA，交DA的延长线于点E，

，

，

∠CAB=90°，

，

，

CA=AB，

，

AD=BE=m，CD=AE=2，

OC+CD=n+1，

OC=n-1（n＞1），

OC+CD=n+m=n+1，

m=1.