题目内容
用换元法解下列方程
(1)x2+2x-2=
;
(2)2x+
-5=0.
(1)x2+2x-2=
| 3 |
| x2+2x |
(2)2x+
| 2x-3 |
(1)令x2+2x=t,则原方程变为:
t-2=
,即t2-2t-3=0,
解得:t1=3,t2=-1,
分别代入x2+2x=t,
得x2+2x=3,
解得x1=1,x2=-3,
得x2+2x=-1,
解得x3=x4=-1,
∴原方程的解是x1=1,x2=-3,x3=x4=-1,
经检验x1=1,x2=-3,x3=x4=-1是方程的根,
故方程的根是:x1=1,x2=-3,x3=x4=-1;
(2)令
=t(t≥0),
则原方程变:t2+t-2=0,
解得:t1=1,t2=-2,
由于t≥0,因此t2=-2不合题意,舍去
将t1=1代入
=t,得
=1,
解之得x=2,
∴原方程的解为:x=2.
t-2=
| 3 |
| t |
解得:t1=3,t2=-1,
分别代入x2+2x=t,
得x2+2x=3,
解得x1=1,x2=-3,
得x2+2x=-1,
解得x3=x4=-1,
∴原方程的解是x1=1,x2=-3,x3=x4=-1,
经检验x1=1,x2=-3,x3=x4=-1是方程的根,
故方程的根是:x1=1,x2=-3,x3=x4=-1;
(2)令
| 2x-3 |
则原方程变:t2+t-2=0,
解得:t1=1,t2=-2,
由于t≥0,因此t2=-2不合题意,舍去
将t1=1代入
| 2x-3 |
| 2x-3 |
解之得x=2,
∴原方程的解为:x=2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
用换元法解下列方程,不恰当的“换元”是( )
A、对于方程
| ||||||
B、对于方程x2+3x-
| ||||||
C、对于方程(x+
| ||||||
D、对于方程(
|
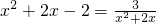 ;
; .
. ,设
,设 =y
=y =8,设y=x2+3x+2
=8,设y=x2+3x+2 )+(x2+
)+(x2+ )=2,设y=
)=2,设y=
 +6=
+6= ,设y=
,设y=