题目内容
已知:如图,在平面直角坐标系中,抛物线y=ax2+c(a≠0)过点A(-6,0)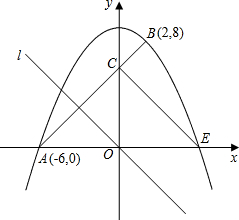 和点B(2,8),线段AB交y轴于点C.
和点B(2,8),线段AB交y轴于点C.
(1)求这条抛物线的解析式;
(2)点M是线段AB上一个动点,过点M作x轴的垂线,交抛物线y=ax2+c于点N,求线段MN的长度的最大值;
(3)设抛物线y=ax2+c与x轴的另一个交点为E,连接CE.过点O作CE的平行线l.在直线l上是否存在点P,在y轴右侧的抛物线y=ax2+c上是否存在点Q,使得四边形COPQ为直角梯形?若存在,请求出P、Q两点的坐标;若不存在,请说明理由.
 解:(1)因为抛物线y=ax2+c(a≠0)过点A(-6,0)、B(2,8),
解:(1)因为抛物线y=ax2+c(a≠0)过点A(-6,0)、B(2,8),所以
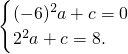
解这个方程组,
得

所以抛物线的解析式为:
 ;
;(2)设直线AB的解析式为:y=kx+b(k≠0),
因为A、B坐标分别为A(-6,0),B(2,8),
所以

解这个方程组,得

所以直线AB的解析式为:y=x+6.
设点M的坐标为(m,y1)(-6≤m≤2),因为点M在线段AB上,所以y1=m+6.
因为MN⊥x轴,我们可设N点坐标为(m,y2).
因为点N在抛物线上,所以
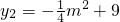 .
.因为点N在点M的上方,
所以MN=y2-y1=
 =
= .
.即MN=
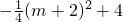 .
.所以当m=-2时,MN长度的最大值为4.
(3)存在.理由如下:
要使四边形COPQ为直角梯形,则四边形COPQ
首先必须为梯形,即需满足CQ∥OP或CO∥PQ.
①若CQ∥OP,
因为O、P两点在直线l上,即有CQ∥l.
又因CE∥l,所以点Q在直线CE上.
因为点Q又在抛物线
 上,
上,所以点Q是直线CE与抛物线
 的交点.
的交点.由已知E是直线CE与抛物线
 的交点,
的交点,所以E就是满足条件的一个Q1点.
在
 中,令y=0,即
中,令y=0,即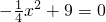 ,解得x1=6,x2=-6(舍去).
,解得x1=6,x2=-6(舍去).所以E(6,0),即Q1(6,0).因为直线CE与抛物线
 的另一个交点在第二象限,故舍去.
的另一个交点在第二象限,故舍去.过点Q1(6,0)作Q1P1⊥l,垂足为P1点,过点P1作P1F⊥x轴,垂足为F.
在直线y=x+6中,令x=0,得y=6.即点C的坐标为(0,6).
在Rt△COQ1中,因为OC=OQ1=6,所以∠CQ1O=45°.
因为CQ1∥l,所以∠Q1OP1=∠CQ1O=45°.
所以△OP1Q1是等腰直角三角形.
所以
 ,
, ,所以P1点的坐标是(3,-3).
,所以P1点的坐标是(3,-3).②CO∥PQ,
因为直线l与直线OC不垂直,所以点C必为直角顶点.CQ⊥y轴.
因为点C的坐标为(0,6),我们可设Q(n,6),
因为点Q在抛物线
 上,
上,所以
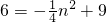 ,
,解得:
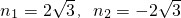 (舍去).
(舍去).得Q2点的坐标为
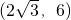 .
.设P2Q2(点P2在直线l上),交x轴于点G,则
 .
.在Rt△OGP2中,∠EOP2=45°,
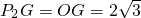 ,
,所以点P2的坐标为
 .
.综上所述,存在满足条件的点P和点Q,坐标分别是P1(3,-3),Q1(6,0)或
 .
.分析:(1)利用待定系数法将A(-6,0)、B(2,8),代入y=ax2+c(a≠0),求出二次函数解析式即可求出;
(2)首先求出直线AB的解析式,设点M的坐标为(m,y1),因为点M在线段AB上,得出y1=m+6,设N点坐标为(m,y2),得出
y2的关系式,相减,利用二次函数的最值求出即可;
(3)根据直角梯形的判定方法,分别由①若CQ∥OP,②CO∥PQ,进行分析得出.
点评:此题主要考查了二次函数的最值以及待定系数法求解析式和梯形的判定方法等知识,此题综合性比较强,用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,直
如图,在平面直角坐标系中,直 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).

