题目内容
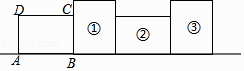
【题目】一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形.在满足条件的所有分割中,若知道九个小矩形中n个小矩形的周长,就一定能算出这个在大矩形的面积,则n的最小值是 ( )
A.3
B.4
C.5
D.6
【答案】A
【解析】解:要算出这个在大矩形的面积,就需要知道大矩形的长和宽.
如图: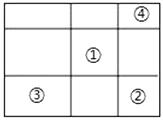
假设已知小矩形①的周长为4x,小矩形③周长为2y,小矩形④周长为2z;
则可得出①的边长以及③和④的邻边和,分别为x、y、z;
设小矩形②的周长为4a,则②的边长为a,可得③、④都有一边长为a
则③和④的另一条边长分别为:y﹣a,z﹣a,
故大矩形的边长分别为:y﹣a+x+a=y+x,z﹣a+x+a=z+x,
故大矩形的面积为:(y+x)(z+x),当x,y,z都为已知数时,即可算出大正方形的面积,
故n的最小值是3.
故选:A.
【考点精析】通过灵活运用推理与论证,掌握一个正确的论证必须满足两个条件:1、论据(前提)是真实的;2、论证方式(推理形式)是正确的(有效的)即可以解答此题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目