题目内容
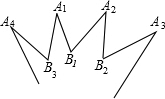
如图所示为一个正n角星的一部分，这正n角星是一个简单的封闭的多边形，其中2n条边相等，角A1，A2，…，An相等，角B1，B2，…，Bn相等，如果锐角A1比锐角B1小10°，那么n是（ ）分析：首先构造出全等三角形，利用三角形内角和定理以及已知条件可得出多边形内角和外角，从而可以求出．
解答：
解：连接B1B2，B2B n
∵正n角星是一个简单的封闭的多边形，
∴△B1B2A2≌△A 3B2Bn，
∴∠1=∠2，
∴∠1+∠2+∠3+∠4=360°．
∠1+∠B2BnA 3+∠A 3=180°，
又∵锐角A1比锐角B1小10°，
∴∠1+∠2+∠3=190°，
∴多边形的内角为；360°-190°=170°，
∴多边形的外角为；10°，正多边形的边数为：360°÷10°=36，
故选：C．
解：连接B1B2，B2B n∵正n角星是一个简单的封闭的多边形，
∴△B1B2A2≌△A 3B2Bn，
∴∠1=∠2，
∴∠1+∠2+∠3+∠4=360°．
∠1+∠B2BnA 3+∠A 3=180°，
又∵锐角A1比锐角B1小10°，
∴∠1+∠2+∠3=190°，
∴多边形的内角为；360°-190°=170°，
∴多边形的外角为；10°，正多边形的边数为：360°÷10°=36，
故选：C．
点评：此题主要考查了正多边形的有关知识，以及等腰三角形和全等三角形的等有关知识．
练习册系列答案
相关题目
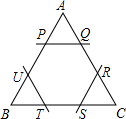如图所示，△ABC是边长为a的正三角形纸张，今在各角剪去一个三角形，使得剩下的六边形PQRSTU为正六边形，则此正六边形的周长为何（ ）| A、2a | ||
| B、3a | ||
C、
| ||
D、
|
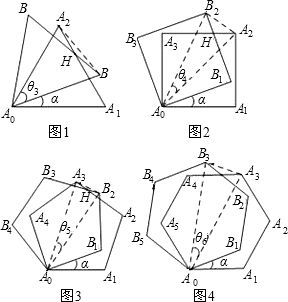
如图所示为一个正n角星的一部分，这正n角星是一个简单的封闭的多边形，其中2n条边相等，角A1，A2，…，An相等，角B1，B2，…，Bn相等，如果锐角A1比锐角B1小10°，那么n是
．
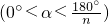