题目内容
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向
向![]() 点运动,速度为
点运动,速度为![]() ;动点
;动点![]() 从
从![]() 点出发,沿线段
点出发,沿线段![]() 向点
向点![]() 运动,速度为
运动,速度为![]() .
.![]() 同时出发,设运动的时间是
同时出发,设运动的时间是![]()
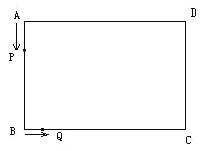
(1)请用含![]() 的代数式表示下列线段的长度,当点
的代数式表示下列线段的长度,当点![]() 在
在![]() 上运动时,
上运动时,![]() ,
,![]() ,当
,当![]() 运动到
运动到![]() 上时,
上时,![]() ,
,![]() .
.
(2)当点![]() 在
在![]() 上运动时,
上运动时,![]() 为何值,能使
为何值,能使![]() ?
?
(3)点![]() 能否追上点
能否追上点![]() ?如果能,求出
?如果能,求出![]() 的值;如果不能,说明理由.
的值;如果不能,说明理由.
【答案】(1)2t,12-2t,2t-12,28-2t;(2)t=4;(3)能,t=12
【解析】
(1)根据动点P从A点出发,沿线段AB,BC向C点运动,速度为每秒2个单位长度,动点Q从B点出发,沿线段BC向C点运动,速度为每秒1个单位长度,再根据运动的时间是t(秒),即可得出答案;
(2)根据PB=BQ,可得出12-2t=t,再求出t的值即可;
(3)根据动点P在BC上时,BP=BQ,得出2t-12=t,求出t的值即可.
解:(1)点P在AB上运动时,AP=2t;PB=12-2t;
当点P运动到BC上时,PB=2t-12;PC=28-2t;
故答案为:2t,12-2t,2t-12,28-2t.
(2)依题意PB=12-2t BQ=t
当PB=BQ时有12-2t=t
解得t=4
∴t=4时PB=BQ
(3)能追上,此时P、Q均在BC上有PB=BQ
依题意PB=2t-12 BQ=t
即2t-12=t
解得t=12
∴t=12时点P能追上点Q

【题目】某玩具厂计划一周生产某种玩具700件,平均每天生产100件,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | -2 | -4 | +13 | -6 | +6 | -3 |
(1)根据记录的数据可知该厂星期四生产玩具 件;
(2)产量最多的一天比产量最少的一天多生产玩具 件;
(3)根据记录的数据可知该厂本周实际生产玩具 件;
(4)该厂实行每周计件工资制,每生产一件玩具可得20元,若超额完成任务,则超过部分每件另奖5元;少生产一件扣4元,那么该厂工人这一周的工资总额是多少元?