题目内容
方程
实数根的情况是（ ）A．仅有三个不同实根
B．仅有两个不同实根
C．仅有一个不同实根
D．无实根
【答案】分析：原方程有意义，则x≠0，把方程去分母、整理可得，x3-2x2+2x-1=0，分解因式得（x-1）（x2-x+1）=0，讨论其根的情况，即可解答．
解答：解：原方程整理得，
x3-2x2+2x-1=0，
∴（x-1）（x2-x+1）=0，
∵方程x2-x+1=0，其△＜0，无解，
∴x2-x+1≠0，
∴x-1=0，即x=1．
故选C．
点评：本题考查了二次函数、反比例函数的性质，主要应用了一元二次方程的根与判别式△的关系．
解答：解：原方程整理得，
x3-2x2+2x-1=0，
∴（x-1）（x2-x+1）=0，
∵方程x2-x+1=0，其△＜0，无解，
∴x2-x+1≠0，
∴x-1=0，即x=1．
故选C．
点评：本题考查了二次函数、反比例函数的性质，主要应用了一元二次方程的根与判别式△的关系．
练习册系列答案
轻松暑假总复习系列答案
相关题目
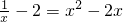实数根的情况是