题目内容
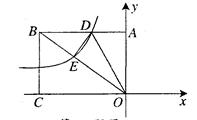
 如图,矩形ABCO的对角线AC、OB交于点A1,直线AC的解析式为y=
如图,矩形ABCO的对角线AC、OB交于点A1,直线AC的解析式为y=
| ||
| 3 |
((
)n-1•
-2
,(
)n-1)
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
((
)n-1•
-2
,(
)n-1)
.| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
分析:根据矩形的性质,以及相似三角形的判定方法,可以证得:△AnCOn∽△ACO,相似比是(
)n.即可求得AnOn,OOn的长,从而求得点An的坐标.
| 1 |
| 2 |
解答:解:在y=
x+2中,令x=0解得:y=2;
令y=0,解得:x=-2
,
则OC=2
,OA=2.
∵A1是矩形ABCO的对角线的交点,OA1∥OA,
∴△A1CO1∽△ACO,相似比是
;
同理,△A2CO2∽△A1CO1,相似比是
;
则△A2CO2∽△ACO,相似比是
=(
)2,
同理:△AnCOn∽△ACO,相似比是(
)n.
∴
=
=(
)n.
∴AnOn=(
)n•OA=(
)n×2=(
)n-1.
OCn=(
)n×OC=(
)n×2
=(
)n-1•
,OOn=2
-(
)n-1•
,
则点An的坐标为((
)n-1•
-2
,(
)n-1)
| ||
| 3 |
令y=0,解得:x=-2
| 3 |
则OC=2
| 3 |
∵A1是矩形ABCO的对角线的交点,OA1∥OA,
∴△A1CO1∽△ACO,相似比是
| 1 |
| 2 |
同理,△A2CO2∽△A1CO1,相似比是
| 1 |
| 2 |
则△A2CO2∽△ACO,相似比是
| 1 |
| 4 |
| 1 |
| 2 |
同理:△AnCOn∽△ACO,相似比是(
| 1 |
| 2 |
∴
| AnOn |
| OA |
| COn |
| OC |
| 1 |
| 2 |
∴AnOn=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
OCn=(
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
则点An的坐标为((
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
点评:本题考查了矩形的性质以及相似三角形的判定与性质,正确理解:△AnCOn∽△ACO,相似比是(
)n是关键.
| 1 |
| 2 |

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目

 如图,矩形ABCO的对角线AC、OB交于点A1,直线AC的解析式为
如图,矩形ABCO的对角线AC、OB交于点A1,直线AC的解析式为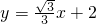 ,过点A1作A1O1⊥OC于O1,过点A1作A1B1⊥BC于B1,得到第二个矩形A1B1CO1,A1C、O1B1交于点A2,过点A2作A2O2⊥OC于O2,过点A2作A2B2⊥BC于B2,得到第三个矩形A2B2CO2,…,依此类推,这样作的第n个矩形对角线交点An的坐标为________.
,过点A1作A1O1⊥OC于O1,过点A1作A1B1⊥BC于B1,得到第二个矩形A1B1CO1,A1C、O1B1交于点A2,过点A2作A2O2⊥OC于O2,过点A2作A2B2⊥BC于B2,得到第三个矩形A2B2CO2,…,依此类推,这样作的第n个矩形对角线交点An的坐标为________.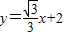 ,过点A1作A1O1⊥OC于O1,过点A1作A1B1⊥BC于B1,得到第二个矩形A1B1CO1,A1C、O1B1交于点A2,过点A2作A2O2⊥OC于O2,过点A2作A2B2⊥BC于B2,得到第三个矩形A2B2CO2,…,依此类推,这样作的第n个矩形对角线交点An的坐标为 .
,过点A1作A1O1⊥OC于O1,过点A1作A1B1⊥BC于B1,得到第二个矩形A1B1CO1,A1C、O1B1交于点A2,过点A2作A2O2⊥OC于O2,过点A2作A2B2⊥BC于B2,得到第三个矩形A2B2CO2,…,依此类推,这样作的第n个矩形对角线交点An的坐标为 .