题目内容
.(本题满分8分)我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售投资收益为:每投入x万元,可获得利润P=-(x-60)2+41(万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润Q=-(100-x)2+(100-x)+160(万元).
(1)若不进行开发,求5年所获利润的最大值是多少?
(2)若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
(3)根据(1)、(2),该方案是否具有实施价值?
解:(1)由P=- (x-60)2+41知,每年只需从100万元中拿出60万元投资,即可获得最大利润41万元,
则不进行开发的5年的最大利润P1=41×5=205(万元) ……(2分)
(2)若实施规划,在前2年中,当x=50时,每年最大利润为:
P=- (50-60)2+41=40万元,前2年的利润为:40×2=80万元,扣除修路后的纯利润为:80-50×2=-20万元. ……(4分)
设在公路通车后的3年中,每年用x万元投资本地销售,而用剩下的(100-x)万元投资外地销售,则其总利润W=[- (x-60)2+41+(- x2+ x+160]×3=-3(x-30)2+3195
当x=30时,W的最大值为3195万元,
∴5年的最大利润为3195-20=3175(万元) ……(7分)
(3)规划后5年总利润为3175万元,不实施规划方案仅为205万元,故具有很大的实施价值. ……(9分)
【解析】略

 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元, 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元,
 时,
时, 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元,
 时,
时,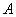 北偏西
北偏西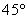 并距该岛
并距该岛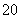 海里的
海里的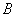 处待命.位于该岛正西方向
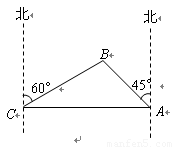
处待命.位于该岛正西方向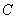 处的某外国商船遭到海盗袭击,船长发现在其北偏东
处的某外国商船遭到海盗袭击,船长发现在其北偏东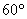 的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿
的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿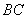 航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置
航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置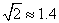 ,
,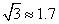 )
)
 元;一月用水超过10吨的用户,10吨水仍按每吨
元;一月用水超过10吨的用户,10吨水仍按每吨 元(
元( )收费.设一户居民月用水
)收费.设一户居民月用水 吨,应收水费
吨,应收水费 元,
元,
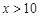 时,
时,